Câu hỏi:
2 năm trước
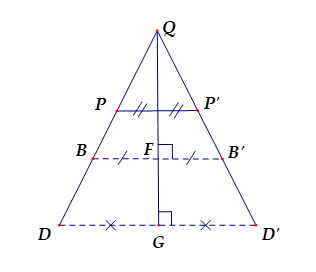
Cho hình vẽ, với \(AD = AE,AG\) là trung trực của \(DE\). Có bao nhiêu cặp đoạn thẳng đối xứng nhau qua trục \(AG\) (các đoạn thẳng thuộc đường thẳng $AD, AE$)? Chọn câu đúng.
Trả lời bởi giáo viên
Đáp án đúng: c
Từ giả thiết ta thấy \(\Delta ADE\) cân tại \(A\) có \(AG\) là đường cao nên \(AG\) cũng là đường trung trực của \(DE.\)
Nên điểm \(D\) và \(E\) đối xứng với nhau qua \(AG\).
Lại có \(BC//DE\) (cùng vuông với \(AG\)) nên suy ra \(\dfrac{{AB}}{{AD}} = \dfrac{{AC}}{{AE}}\) (định lý Ta-lét)
Mà \(AD = AE\left( {gt} \right) \Rightarrow AB = AC\). Do đó \(\Delta ABC\) cân tại \(A\) có \(AF\) là đường cao nên \(AF\) cũng là đường trung trực của \(BC\).
Từ đó điểm \(B,C\) đối xứng nhau qua \(AG\).
Như vậy:
+ Hai đoạn thẳng \(BD,CE\) đối xứng nhau qua \(AG\)
+ Hai đoạn thẳng \(AB,AC\) đối xứng nhau qua \(AG\)
+ Hai đoạn thẳng \(AD,AE\) đối xứng nhau qua \(AG\)
Hướng dẫn giải:
Bước 1: Ta sử dụng định nghĩa: “Hai điểm \(A,B\) gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \(d\) là đường trung trực của đoạn thẳng nối hai điểm đó” để tìm các cặp điểm đối xứng nhau qua đường thẳng \(m\).
Bước 2: Từ đó suy ra các đoạn thẳng đối xứng nhau qua đường thẳng \(m\).
