Trả lời bởi giáo viên
Đáp án đúng: d
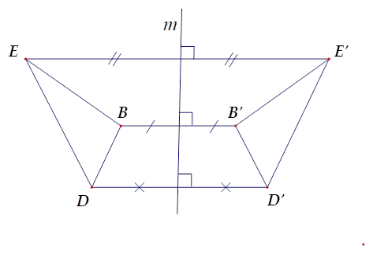
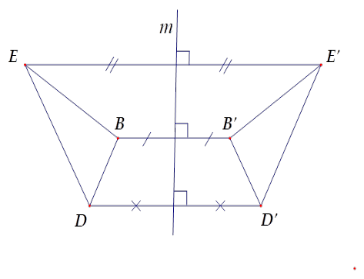
Từ hình vẽ ta có \(A\) và \(A'\) đối xứng nhau qua đường thẳng \(m\); \(B\) và \(B'\) đối xứng nhau qua đường thẳng \(m\); \(C\) và \(C'\) đối xứng nhau qua đường thẳng \(m\).
Suy ra hai đoạn thẳng \(EB\) và \(E'B'\) đối xứng nhau qua \(m\).
Hai đoạn thẳng \(DB\) và \(D'B'\) đối xứng nhau qua \(m\).
Hai tam giác \(DEB\) và \(D'E'B'\) đối xứng nhau qua \(m\).
Hai đoạn thẳng \(DE\) và \(D'E'\) đối xứng nhau qua \(m\) nên D sai.
Hướng dẫn giải:
Bước 1: Ta sử dụng định nghĩa: “ Hai điểm $A,B$ gọi là đối xứng với nhau qua đường thẳng $d$ nếu $d$ là đường trung trực của đoạn thẳng nối hai điểm đó ” để tìm các cặp điểm đối xứng nhau qua đường thẳng \(m\) .
Bước 2: Từ đó suy ra các đoạn thẳng và tam giác đối xứng nhau qua đường thẳng \(m\) .