Câu hỏi:
2 năm trước
Cho tam giác \(ABC\), trong đó \(AB = 8\,cm,AC = 10\,cm\). Vẽ hình đối xứng với tam giác \(ABC\) qua trục là cạnh \(BC\). Chu vi của tứ giác tạo thành là:
Trả lời bởi giáo viên
Đáp án đúng: c
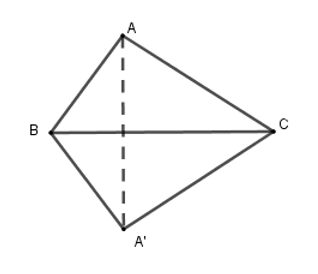
Gọi \(A'\) là điểm đối xứng với \(A\) qua \(BC\). Khi đó tam giác \(A'BC\) đối xứng với tam giác \(ABC\) qua \(BC\).
Tứ giác tạo thành là \(ABCA'\).
Ta có: \(A'B = AB = 8\,cm\) (vì \(A'B\) và \(AB\) đối xứng nhau qua \(BC\)).
\(A'C = AC = 10\,cm\) (vì \(A'C\) và \(AC\) đối xứng nhau qua \(BC\)).
Chu vi tứ giác \(ABCA'\) là \(P = AB + AC + A'B + A'C\)\( = 8 + 10 + 8 + 10 = 36\,cm\).
Hướng dẫn giải:
Bước 1: Ta sử dụng chú ý: “Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.”
Bước 2: Từ đó suy ra độ dài các cạnh còn lại rồi tính chu vi tứ giác.