Trả lời bởi giáo viên
Đáp án đúng: a
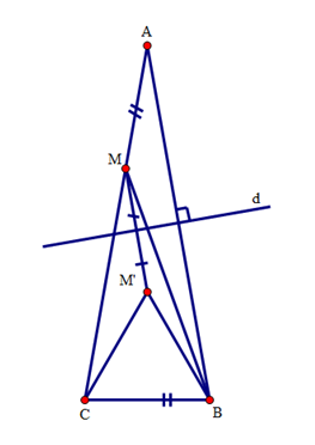
Do tính chất đối xứng qua d, ta có AM=BM′.
Mà AM=BC(gt) nên BM′=BC.
Ta lại có: ^M′BA=^MAB=200 (do M,A đối xứng với M′,B qua d).
Suy ra ^M′BC=ˆB−200=800−200=600.
Xét tam giác M′BC có BM′=BC, ^M′BC=600 do đó tam giác M′BC là tam giác đều.
Hướng dẫn giải:
Sử dụng tính chất đối xứng của điểm, đoạn thẳng qua đường thẳng.
Chứng minh tam giác cân có một góc bằng 60∘.
