Cho hình bình hành \(ABCD\). Gọi \(E,F\) theo thứ tự là trung điểm của \(AD,{\rm{ }}BC\). Đường chéo \(AC\) cắt \(BE,DF\) theo thứ tự ở \(K,I{\rm{ }}\). Chọn khẳng định đúng nhất.

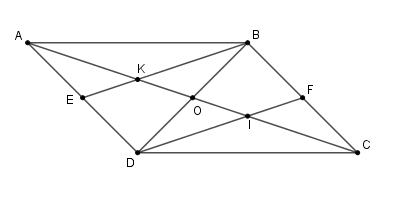
Gọi \(O\) là giao điểm của \(AC,BD\).

Vì \(ABCD\) là hình bình hành nên \(AC,BD\) giao nhau tại trung điểm \(O\) mỗi đường, hay \(AO = CO = \dfrac{{AC}}{2}\).

Xét tam giác \(ABD\) có \(BE,AO\) là hai đường trung tuyến cắt nhau tại \(K\) nên \(K\) là trọng tâm \(\Delta ABD\).

Suy ra \(AK = \dfrac{2}{3}AO = \dfrac{2}{3}.\dfrac{1}{2}AC = \dfrac{1}{3}AC\)  (1)

Xét tam giác \(CBD\) có \(DF,CO\) là hai đường trung tuyến cắt nhau tại \(I\) nên \(I\) là trọng tâm \(\Delta CBD\).

Suy ra \(CI = \dfrac{2}{3}CO = \dfrac{2}{3}.\dfrac{1}{2}AC = \dfrac{1}{3}AC\)  (2)

Lại có: \(AK + KI + CI = AC \Rightarrow KI = AC - AK - CI\) \( = AC - \dfrac{1}{3}AC - \dfrac{1}{3}AC = \dfrac{1}{3}AC\) (3)

Từ (1), 2) và (3) suy ra: \(AK = KI = IC\).