Câu hỏi:
2 năm trước
Cho tứ giác \(ABCD\) có \(\widehat A = 80^\circ \). Tổng số đo các góc ngoài đỉnh \(B,C,D\) bằng:
Trả lời bởi giáo viên
Đáp án đúng: b
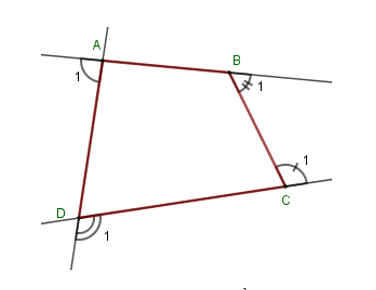
Gọi góc ngoài tại bốn đỉnh \(A,B,\,C,\,D\) của tứ giác \(ABCD\) lần lượt là \(\widehat {{A_1}};\,\widehat {{B_1}};\,\widehat {{C_1}};\,\widehat {{D_1}}\). Khi đó ta có:
\(\widehat A + \widehat {{A_1}} = 180^\circ \)\(\Rightarrow \widehat {{A_1}} = 180^\circ - \widehat A \)\(= 180^\circ - 80^\circ = 100^\circ \).
Theo kết quả các câu trước ta có \(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 360^\circ \)\( \Rightarrow \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 360^\circ - \widehat {{A_1}} = 360^\circ - 100^\circ = 260^\circ \).
Vậy \(\widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 260^\circ \).
Hướng dẫn giải:
Bước 1: Tính góc ngoài tại đỉnh \(A\).
Bước 2: Từ câu \(6\) ta suy ra “tổng số đo góc ngoài tại bốn đỉnh của một tứ giác là \(360^\circ \)”. Từ đó tính tổng số đo các góc ngoài đỉnh \(B,C,D\).
