Câu hỏi:
2 năm trước
Cho tứ giác \(ABCD\) có \(\widehat {A\,\,} = 65^\circ \;;\,\,\widehat {B\,\,} = 117^\circ ;\,\,\widehat {C\,\,} = 71^\circ \). Số đo góc ngoài tại đỉnh \(D\) bằng:
Trả lời bởi giáo viên
Đáp án đúng: c
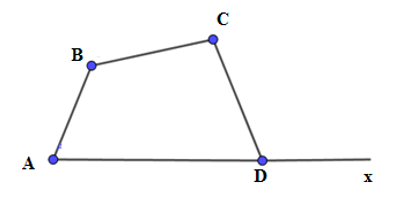
\(\widehat {CDx}\) là góc ngoài đỉnh D.
Tứ giác ABCD có: \(\widehat {D\,} = 360^\circ - \left( {\widehat {A\,\,} + \widehat {B\,\,} + \widehat {C\,\,}} \right)\)\( = 360^\circ - \left( {65^\circ + 117^\circ + 71^\circ } \right) = 107^\circ \)
Vì \(\widehat {ADC}\) và \(\widehat {CDx}\) là hai góc kề bù nên \(\widehat {CDx} = 180^\circ - \widehat {D\,} = 180^\circ - 107^\circ = 73^\circ \).
Hướng dẫn giải:
+ Ta sử dụng định lý về tổng các góc trong tứ giác: Tổng các góc của một tứ giác bằng \(360^\circ \) để tính góc \(D\).
+ Từ đó suy ra số đo góc ngoài tại \(D\) là \(180^\circ - \widehat D\).
