Câu hỏi:
2 năm trước
Tứ giác \(ABCD\) có \(AB = BC,CD = DA,\;\widehat B = {100^0};\;\widehat D = {70^0}\). Tính \(\widehat A;\widehat C.\)
Trả lời bởi giáo viên
Đáp án đúng: a
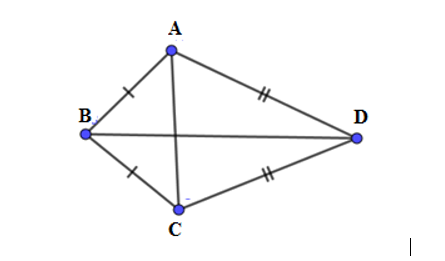
Xét tam giác \(ABC\) có: \(\widehat B = 100^\circ ;AB = BC \Rightarrow \Delta ABC\)cân tại \(B\) \( \Rightarrow \widehat {BAC} = \widehat {BCA} = \dfrac{{180^\circ - 100^\circ }}{2} = 40^\circ \).
Xét tam giác \(ADC\) có \(CD = DA \Rightarrow \Delta ADC\) cân tại \(D\) có \(\widehat {ADC} = 70^\circ \) nên \(\widehat {DAC} = \widehat {DCA} = \dfrac{{180^\circ - 70^\circ }}{2} = 55^\circ \).
Từ đó ta có: \(\widehat A = \widehat {BAD} = \widehat {BAC} + \widehat {CAD} = 40^\circ + 55^\circ = 95^\circ \).
Và \(\widehat C = \widehat {BCD} = \widehat {BCA} + \widehat {ACD} = 40^\circ + 55^\circ = 95^\circ \).
Nên \(\widehat A = \widehat C = 95^\circ \).
Hướng dẫn giải:
Ta sử dụng tính chất tam giác cân và tổng ba góc trong tam giác bằng \(180^\circ \) .
