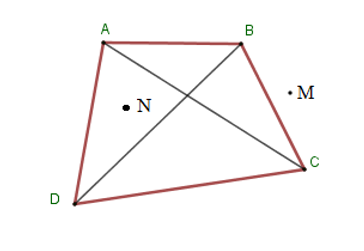
Cho tứ giác$ABCD$. Gọi $O$ là giao điểm của hai đường chéo $AC$ và$BD$ . Khẳng định nào sau đây là đúng nhất.

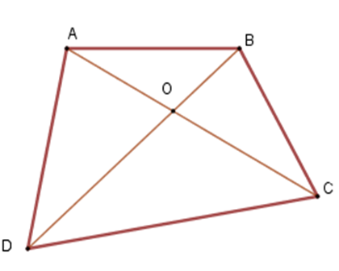
+ Xét tam giác \(OAB\) ta có \(OA + OB > AB\)(vì trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại) .

Tương tự ta có \(OC + OD > CD;\,OB + OC > BC;\,OA + OD > AD\)

Cộng vế với vế ta được \(OA + OB + OC + OD + OB + OC + OA + OD > AB + BC + CD + AD\)

\( \Leftrightarrow 2\left( {OA + OB + OC + OD} \right) > AB + BC + CD + DA\) \( \Leftrightarrow OA + OB + OC +OD> \dfrac{{AB + BC + CD + DA}}{2}\)  nên B đúng.

+ Xét tam giác \(ABC\) ta có \(AB + BC > AC\) (vì trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại) .

Tương tự ta có \(BC + CD > BD;\,CD + DA > AC;\,AD + DB > BD\)

Cộng vế với vế ta được: \(AB + BC + BC + CD + CD + DA + DA + AB > AC + BD + AC + BD\)

\( \Leftrightarrow 2\left( {AB + BC + CD + DA} \right) > 2\left( {AC + BD} \right)\) \( \Leftrightarrow AB + BC + CD + DA > AC + BD\) mà \(AC + BD = OA + OC + OB + OD\) nên \(AB + BC + CD + DA > OA + OB + OC + OD\) nên A đúng.

Vậy cả A, B đều đúng.