Trả lời bởi giáo viên
Đáp án đúng: d
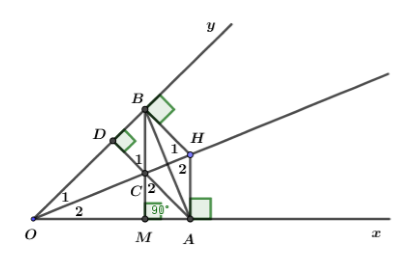
Xét hai tam giác vuông \(HBO\) và \(HAO\) ta có:
Cạnh huyền \(OH\,chung\)
Góc nhọn \({O_1} = {O_2}\)
\( \Rightarrow \Delta HBO = \Delta HAO\,\) (cạnh huyền-góc nhọn)
Do đó: \(OA = OB\) (cạnh tương ứng)
Xét tam giác \(OAB\) cân tại O do \(OA = OB\) (cmt)
Mà \(AD \bot BO\) \( \Rightarrow AD\) là đường cao.
C nằm trên tia phân giác góc O. Hay OC là đường phân giác góc O.
Trong một tam giác cân đường phân giác cũng chính là đường cao.
Mặt khác CO giao với AD tại C.
\( \Rightarrow C\) là trực tâm của tam giác OAB.
Do đó BC là đường cao.
Hay \(BC \bot OA\) hay \(BC \bot {\rm{Ox}}\)
Hướng dẫn giải:
+) Chứng minh hai tam giác bằng nhau rồi suy ra cặp cạnh bằng nhau
+) Chứng minh C là trực tâm của tam giác \(OAB\).
Câu hỏi khác
- Đề thi khảo sát chất lượng đầu năm - Đề số 1 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 2 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 3 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 5 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 4 toán 8 có lời giải
