Trả lời bởi giáo viên
Đáp án đúng: a
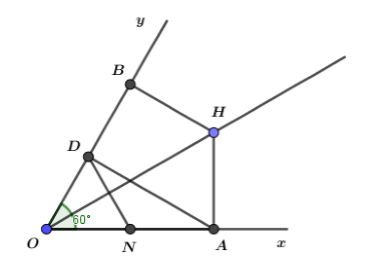
Gọi N là trung điểm của OA, khi đó trong tam giác vuông AOD (vuông tại D)
Khi đó \(D{\rm N} = O{\rm N} = \dfrac{{OA}}{2}\) (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
\( \Rightarrow \Delta {\rm N}OD\) cân tại N (1)
Mặt khác \(\widehat {AOD} = \widehat {xOy} = {60^0}\) (2)
Từ (1) và (2), suy ra \(\Delta {\rm N}OD\) là tam giác đều.
\( \Rightarrow OD = O{\rm N}\) mà \(O{\rm N} = \dfrac{1}{2}OA\)
\( \Rightarrow OD = \dfrac{1}{2}OA\,\,hay\,\,OA = 2OD\).
Hướng dẫn giải:
Chứng minh khi \(\widehat {xOy} = {60^0}\) thì tam giác \({\rm N}OD\) là tam giác đều, từ đó suy ra \(OD = O{\rm N}\).
Sau đó lập luận để có mối quan hệ đúng.
Câu hỏi khác
- Đề thi khảo sát chất lượng đầu năm - Đề số 1 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 2 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 3 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 5 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 4 toán 8 có lời giải
