Tính giá trị biểu thức sau bằng cách hợp lý:
\(A = \dfrac{3}{4}.\dfrac{5}{{14}} + \dfrac{6}{7}:\dfrac{4}{3} - 1\dfrac{1}{7}:1\dfrac{1}{3}\).
Ta có: \(A = \dfrac{3}{4}.\dfrac{5}{{14}} + \dfrac{6}{7}:\dfrac{4}{3} - 1\dfrac{1}{7}:1\dfrac{1}{3}\)
\(\begin{array}{l} = \dfrac{3}{4}.\dfrac{5}{{14}} + \dfrac{6}{7}.\dfrac{3}{4} - \dfrac{8}{7}:\dfrac{4}{3}\\ = \dfrac{3}{4}.\dfrac{5}{{14}} + \dfrac{6}{7}.\dfrac{3}{4} - \dfrac{8}{7}.\dfrac{3}{4}\\ = \dfrac{3}{4}\left( {\dfrac{5}{{14}} + \dfrac{6}{7} - \dfrac{8}{7}} \right)\\ = \dfrac{3}{4}\left( {\dfrac{5}{{14}} - \dfrac{2}{7}} \right)\\ = \dfrac{3}{4}.\dfrac{1}{{14}}\\ = \dfrac{3}{{56}}\end{array}\).
Vậy \(A = \dfrac{3}{{56}}.\)
Tìm \(x\) biết \(\left( { - 1\dfrac{3}{5} + x} \right).\dfrac{{14}}{{15}} = 2\dfrac{1}{3}\).
Ta có: \(\left( { - 1\dfrac{3}{5} + x} \right).\dfrac{{14}}{{15}} = 2\dfrac{1}{3}\)
\(\begin{array}{l} \Leftrightarrow \left( { - \dfrac{8}{5} + x} \right).\dfrac{{14}}{{15}} = \dfrac{7}{3}\\ \Leftrightarrow - \dfrac{8}{5} + x = \dfrac{7}{3}:\dfrac{{14}}{{15}}\\ \Leftrightarrow - \dfrac{8}{5} + x = \dfrac{7}{3}.\dfrac{{15}}{{14}}\\ \Leftrightarrow - \dfrac{8}{5} + x = \dfrac{5}{2}\\ \Leftrightarrow x = \dfrac{5}{2} + \dfrac{8}{5}\\ \Leftrightarrow x = \dfrac{{25 + 16}}{{10}}\\ \Leftrightarrow x = \dfrac{{41}}{{10}}\end{array}\).
Cho các đa thức:
\(\begin{array}{l}f\left( x \right) = {x^3} - 2{x^2} + 3x + 1\\g\left( x \right) = {x^3} + x - 1\\h\left( x \right) = 2{x^2} - 1\end{array}\).
Tính: \(f\left( x \right) - g\left( x \right) + h\left( x \right)\).
\(\begin{array}{l}\,f\left( x \right) = {x^3} - 2{x^2} + 3x + 1\\g\left( x \right) = {x^3} + x - 1\\h\left( x \right) = 2{x^2} - 1\\ \Rightarrow f\left( x \right) - g\left( x \right) + h\left( x \right)\\ = {x^3} - 2{x^2} + 3x + 1 - \left( {{x^3} + x - 1} \right) + \left( {2{x^2} - 1} \right)\\ = \,{x^3} - 2{x^2} + 3x + 1 - {x^3} - x + 1 + 2{x^2} - 1\\ = \left( {{x^3} - {x^3}} \right) + \left( { - 2{x^2} + 2{x^2}} \right) + \left( {3x - x} \right) + 1 + 1 - 1\\ = 2x + 1\end{array}\).
Vậy \(f\left( x \right) - g\left( x \right) + h\left( x \right) = 2x + 1.\)
Cho các đa thức:
\(\begin{array}{l}f\left( x \right) = {x^3} - 2{x^2} + 3x + 1\\g\left( x \right) = {x^3} + x - 1\\h\left( x \right) = 2{x^2} - 1\end{array}\).
Tìm x sao cho \(f\left( x \right) - g\left( x \right) + h\left( x \right) = 0.\)
Ta có:
\(\begin{array}{l}f\left( x \right) - g\left( x \right) + h\left( x \right) = 0\\ \Leftrightarrow 2x + 1 = 0\\ \Leftrightarrow 2x\,\,\,\,\,\,\,\, = - 1\\ \Leftrightarrow \,\,\,\,x\,\,\,\,\,\,\,\, = \dfrac{{ - 1}}{2}\end{array}\).
Vậy \(x = \dfrac{{ - 1}}{2}.\)
Cho góc nhọn \(xOy.\) Điểm H nằm trên tia phân giác của góc \(xOy.\) Hạ \(HA \,\bot \,{\rm{Ox,}}\,{\rm{HB}} \,\bot \,{\rm{Oy}}\) \(\left( {A \in {\rm{Ox}},\,B \in Oy} \right)\). Gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OH.
Tam giác \(HAB\) là tam giác:
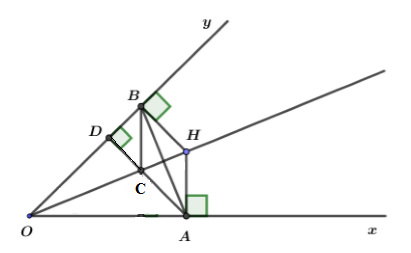
Vì \(H\) nằm trên tia phân giác của góc \(xOy\)
mà \(HA \,\bot \,{\rm{Ox,}}\,{\rm{HB}} \,\bot \,{\rm{Oy}}\) nên ta có:
\(HA = HB\) (tính chất các điểm thuộc tia phân giác)
\( \Rightarrow \Delta HAB\) cân tại \(H\).
Cho góc nhọn \(xOy.\) Điểm H nằm trên tia phân giác của góc \(xOy.\) Hạ \(HA \,\bot \,{\rm{Ox,}}\,{\rm{HB}} \,\bot \,{\rm{Oy}}\) \(\left( {A \in {\rm{Ox}},\,B \in Oy} \right)\). Gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OH.
Chọn câu đúng.
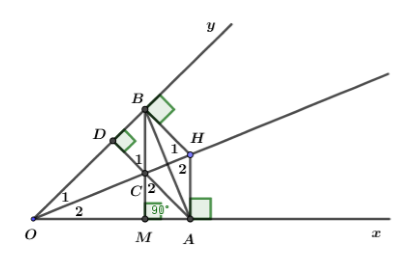
Xét hai tam giác vuông \(HBO\) và \(HAO\) ta có:
Cạnh huyền \(OH\,chung\)
Góc nhọn \({O_1} = {O_2}\)
\( \Rightarrow \Delta HBO = \Delta HAO\,\) (cạnh huyền-góc nhọn)
Do đó: \(OA = OB\) (cạnh tương ứng)
Xét tam giác \(OAB\) cân tại O do \(OA = OB\) (cmt)
Mà \(AD \bot BO\) \( \Rightarrow AD\) là đường cao.
C nằm trên tia phân giác góc O. Hay OC là đường phân giác góc O.
Trong một tam giác cân đường phân giác cũng chính là đường cao.
Mặt khác CO giao với AD tại C.
\( \Rightarrow C\) là trực tâm của tam giác OAB.
Do đó BC là đường cao.
Hay \(BC \bot OA\) hay \(BC \bot {\rm{Ox}}\)
Cho góc nhọn \(xOy.\) Điểm H nằm trên tia phân giác của góc \(xOy.\) Hạ \(HA \,\bot \,{\rm{Ox,}}\,{\rm{HB}} \,\bot \,{\rm{Oy}}\) \(\left( {A \in {\rm{Ox}},\,B \in Oy} \right)\). Gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OH.
Khi \(\widehat {xOy} = {60^0}\) thì ta có:
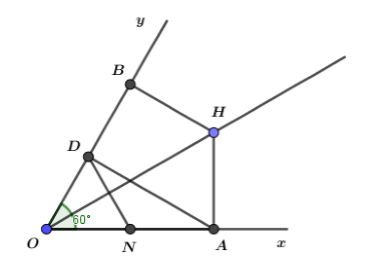
Gọi N là trung điểm của OA, khi đó trong tam giác vuông AOD (vuông tại D)
Khi đó \(D{\rm N} = O{\rm N} = \dfrac{{OA}}{2}\) (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
\( \Rightarrow \Delta {\rm N}OD\) cân tại N (1)
Mặt khác \(\widehat {AOD} = \widehat {xOy} = {60^0}\) (2)
Từ (1) và (2), suy ra \(\Delta {\rm N}OD\) là tam giác đều.
\( \Rightarrow OD = O{\rm N}\) mà \(O{\rm N} = \dfrac{1}{2}OA\)
\( \Rightarrow OD = \dfrac{1}{2}OA\,\,hay\,\,OA = 2OD\).
Số cây của ba tổ trồng tỉ lệ với số học sinh của mỗi tổ, tổng số cây ba tổ trồng được là \(135\) cây. Tìm số cây của tổ 3 đã trồng, biết tổ 1 có 7 bạn, tổ 2 có 8 bạn và tổ 3 có 12 bạn.
Gọi số cây tổ 1, tổ 2, tổ 3 trồng được lần lượt là: \(x,y,z\,\,\left( {x;y;z \in {\mathbb{N}^*}} \right)\) (cây).
Ba tổ trồng được \(135\) cây nên ta có \(x + y + z = 135\).
Vì số cây của ba tổ trồng tỉ lệ với số học sinh của mỗi tổ nên \(\dfrac{x}{7} = \dfrac{y}{8} = \dfrac{z}{{12}}\).
Áp dụng tính chất dãy tỉ số bằng nhau ta có \(\dfrac{x}{7} = \dfrac{y}{8} = \dfrac{z}{{12}} = \dfrac{{x + y + z}}{{7 + 8 + 12}} = \dfrac{{135}}{{27}} = 5\) (vì \(x + y + z = 135\)).
Suy ra:
+) \(\dfrac{x}{7} = 5 \Leftrightarrow x = 5.7 = 35\)
+) \(\dfrac{y}{8} = 5 \Leftrightarrow y = 5.8 = 40\)
+) \(\dfrac{z}{{12}} = 5 \Leftrightarrow z = 5.12 = 60\)
Vậy số cây tổ 3 trồng được là \(60\) cây.
Tìm giá trị nhỏ nhất của biểu thức \({\left( {{x^2} - 9} \right)^2} + \left| {y - 3} \right| - 1\).
Đặt \(A = {\left( {{x^2} - 9} \right)^2} + \left| {y - 3} \right| - 1\).
Ta có:
\(\begin{array}{l}{\left( {{x^2} - 9} \right)^2} \ge 0;\,\left| {y - 3} \right|\,\, \ge 0\\ \Rightarrow {\left( {{x^2} - 9} \right)^2} + \left| {y - 3} \right| - 1 \ge 0 + 0 - 1\\ \Rightarrow {\left( {{x^2} - 9} \right)^2} + \left| {y - 3} \right| - 1 \ge - 1\end{array}\).
Hay \(A \ge - 1\). Dấu xảy ra khi và chỉ khi: \(\left\{ \begin{array}{l}{x^2} - 9 = 0\\y - 3 = 0\end{array} \right.\) hay \(x = - 3\) hoặc \(x = 3\) và \(y = 3\)
Vậy giá trị nhỏ nhất của A là: \(A = - 1\) khi \(x = - 3;y = 3\) hoặc \(x = y = 3\).

