Tứ giác $AGCH$ là hình gì?

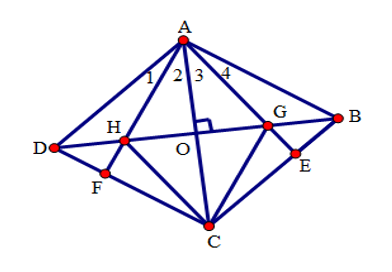
Gọi O là giao điểm của AC và BD thì $AC \bot BD$ (do O là giao điểm của hai đường chéo của hình thoi)

Áp dụng định nghĩa, tính chất về góc và giả thiết vào hình thoi ABCD, ta được:

$AB = AD,\widehat {\,\,B} = \widehat D,\,\,BE = DF.$

Từ đó suy ra $\Delta ABE = \Delta ADF(c.g.c)$

Suy ra $\widehat {{A_1}} = \widehat {{A_4}}$ (hai góc tương ứng).

Mà AC là phân giác của $\widehat A \Rightarrow \widehat {{A_2}} = \widehat {{A_3}}.$  (1)

Do đó AO là phân giác của $\widehat {HAG}.$

Xét tam giác AGH có AO là đường cao, đồng thời là đường phân giác nên tam giác AGH cân tại A.

Suy ra: HO = OG  (2)

Do ABCD là hình thoi nên AO = OC (tính chất đường chéo của hình thoi)  (3)

Từ (1), (2), (3) suy ra: AHCG là hình thoi.