Cho tứ giác ABCD có \(\widehat C = {50^ \circ },\widehat D = {80^ \circ }\), AD = BC. Gọi E, F lần lượt là trung điểm của các cạnh AB và CD. Tính số đo góc EFC.

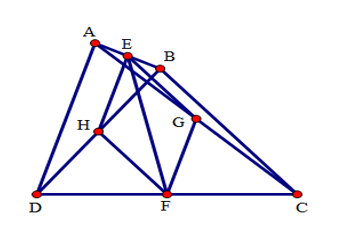
Gọi G, H lần lượt là trung điểm của AC, BD.

Vì E, G lần lượt là trung điểm của AB, AC nên EG là đường trung bình của tam giác ABC. Suy ra \(EG = \dfrac{1}{2}BC;\,\,EG//BC.\)

Chứng minh tương tự ta cũng có:

\(GF = \dfrac{1}{2}AD,FH = \dfrac{1}{2}BC,HE = \dfrac{1}{2}AD;\,\,GF//AD;\,\,FH//BC;\,\,HE//AD.\)

Mà AD = BC (gt), nên EG = GF = FH = HE.

Suy ra: tứ giác EGFH là thoi.

Suy ra EF là tia phân giác của góc \(\widehat {HFG} \Rightarrow \widehat {EFG} = \dfrac{1}{2}\widehat {HFG}.\)

\(\widehat {GFC} = \widehat {ADC} = {80^0}\,\left( {do\,\,GF//AD} \right);\,\,\widehat {HFD} = \widehat {BCD} = {50^0}\,\,\,\left( {do\,\,\,FH//BC} \right).\)

Do đó \(\widehat {HFG} = {180^0} - \left( {\widehat {GFC} + \widehat {HFD}} \right) = {50^0} \Rightarrow \widehat {EFG} = \dfrac{1}{2}{.50^0} = {25^0}\).

Vậy \(\widehat {EFC} = \widehat {EFG} + \widehat {GFC} = {25^0} + {80^0} = {105^0}\).