Cho hình bình hành \(ABCD.\) Gọi E, F là trung điểm của các cạnh \(AD\) và \(BC.\) Các đường BE, DE cắt các đường chéo AC tại P và Q. Tứ giác EPFQ là hình thoi nếu góc ACD bằng:

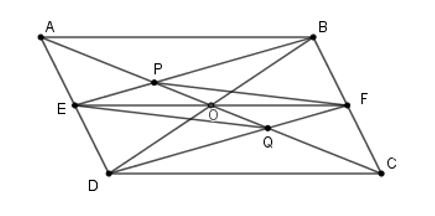
Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\)

Vì \(ABCD\) là hình hình hành nên \(O\) là trung điểm của \(AC,BD.\)

Xét tứ giác \(EDFB\) có \(\left\{ \begin{array}{l}ED//FB\\ED = FB\left( { = \dfrac{1}{2}AD} \right)\end{array} \right.\)  nên \(EDFB\) là hình bình hành, suy ra \(\left\{ \begin{array}{l}BE = DF\\BE//DF\end{array} \right.\)

Xét tam giác \(ABD\) có \(P\) là giao điểm hai đường trung tuyến nên \(P\) là trọng tâm \(\Delta ABD \Rightarrow EP = \dfrac{1}{3}BE\)

Xét tam giác \(CBD\) có \(Q\) là giao điểm hai đường trung tuyến nên \(Q\) là trọng tâm \(\Delta CBD \Rightarrow QF = \dfrac{1}{3}DF\)

Mà \(BE = DF\left( {cmt} \right) \Rightarrow EP = QF\)

Xét tứ giác \(EPFQ\) có \(\left\{ \begin{array}{l}EP = QF\\EP//QF\end{array} \right. \Rightarrow EPFQ\) là hình bình hành.

Để hình bình hành \(EPFQ\) là hình thoi thì \(EF \bot PQ\).

Mà \(EF//CD\) (do \(E\) là trung điểm \(AD,F\) là trung điểm \(BC\)).

Nên \(PQ \bot CD\) hay \(AC \bot CD \Rightarrow \widehat {ACD} = 90^\circ \).