Câu hỏi:
2 năm trước
Tứ giác \(ABCD\) có \(AB = CD.\) Gọi \(M,N\) theo thứ tự là trung đểm của \(BC,AD.\) Gọi \(I,K\) theo thứ tự là trung điểm của \(AC,BD.\) Chọn câu đúng nhất.
Trả lời bởi giáo viên
Đáp án đúng: c
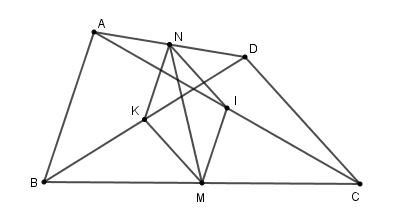
Từ giả thiết ta có: \(KM;IM;IN;KN\) lần lượt là các đường trung bình của các tam giác \(BCD,CAB,ADC,DBA\). (định nghĩa đường trung bình).
Đặt \(BA = CD = 2a\).
Áp dụng định lý đường trung bình và giả thiết vào bốn tam giác trên ta được:
\(MK = \dfrac{1}{2}CD = a;IM = \dfrac{1}{2}AB = a;NI = \dfrac{1}{2}CD = a;KN = \dfrac{1}{2}AB = a\).
Suy ra \(MK = KN = NI = IM\).
Tứ giác \(KMIN\) có bốn cạnh bằng nhau nên là hình thoi.
Áp dụng tính chất về đường chéo vào hình thoi \(KMIN\) ta được: \(MN \bot KI;MN\) là đường phân giác \(\widehat {KMI}\).
Hướng dẫn giải:
+ Sử dụng tính chất đường trung bình của tam giác.
+ Sử dụng dấu hiệu nhận biết hình thoi và tính chất hình thoi.
