Cho hình thoi $ABCD$ có chu vi bằng $16\,cm$ , đường cao $AH$ bằng $2\,cm$ . Tính các góc của hình thoi. Hãy chọn câu đúng.
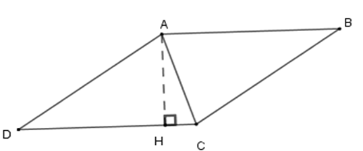
Vì chu vi hình thoi là \(16\,cm\) nên cạnh hình thoi có độ dài \(16:\,4 = 4\,cm\) . Suy ra \(AD = 4\,cm\) .
Xét tam giác \(AHD\) vuông tại \(H\) có \(AH = \dfrac{1}{2}AD \Rightarrow \widehat {ADH} = 30^\circ \) (tính chất)
Suy ra \(\widehat {DAB} = 180^\circ - \widehat {ADC} = 180^\circ - 30^\circ = 150^\circ \) (vì \(ABCD\) là hình thoi)
Nên hình thoi \(ABCD\) có \(\widehat D = \widehat B = 30^\circ ;\,\widehat A = \widehat C = 150^\circ \) (vì hai góc đối bằng nhau).
Cho hình thang$ABCD$ . Gọi $M,N,P,Q$ lần lượt là trung điểm của$AB,BC,CD,DA$ . Hình thang $ABCD$ có thêm điều kiện gì thì $MNPQ$ là hình thoi. Hãy chọn câu đúng
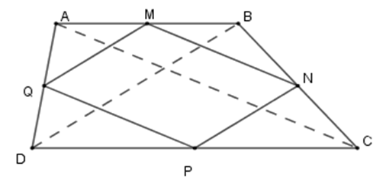
+ Xét tam giác \(ABC\) có \(MN\) là đường trung bình nên \(MN{\rm{//}}AC;\,MN = \dfrac{1}{2}AC\) (1)
Tương tự ta có \(PQ\) là đường trung bình tam giác \(ADC\) nên \(PQ{\rm{//}}AC;\,PQ = \dfrac{1}{2}AC\) (2)
Từ (1) và (2) suy ra \(MN{\rm{//}}PQ;\,MN = PQ \Rightarrow MNPQ\) là hình bình hành.
Để hình bình hành \(MNPQ\) là hình thoi ta cần có \(MN = MQ\).
Mà \(MN = \dfrac{1}{2}AC\,\left( {cmt} \right);\,MQ = \dfrac{1}{2}BD\) (do \(MQ\) là đường trung bình tam giác \(ABD\) )
Suy ra \(AC = BD\) .
Vậy để hình bình hành \(MNPQ\) là hình thoi thì \(AC = BD\).
Cho hình thoi có độ dài hai đường chéo là $24\,cm$ và $10\,cm$ . Tính độ dài cạnh hình thoi.
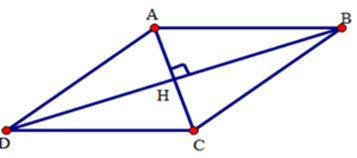
Giả sử $ABCD$ là hình thoi có hai đường chéo cắt nhau tại $H$ và $AC = 10cm,BD = 24cm.$
Do $ABCD$ là hình thoi nên:
\(AC \bot BD;AH = \dfrac{1}{2}AC \)\(= \dfrac{1}{2}.10 = 5\left( {cm} \right);\)\(\,\,HB = \dfrac{1}{2}BD = \dfrac{1}{2}.24 = 12\left( {cm} \right).\)
Xét tam giác $AHB$ vuông tại $H$ ta có: $A{B^2} = A{H^2} + H{B^2} = {5^2} + {12^2} = 25 + 144 = 169$
Suy ra $AB = 13\,cm$.
Cho tam giác $ABC$ vuông ở \(A\) , trung tuyến $AM$ . Gọi $D$ là trung điểm của $AB$ , $M'$ là điểm đối xứng với $M$ qua $D$ .
Tứ giác \(AMBM'\) là hình gì?
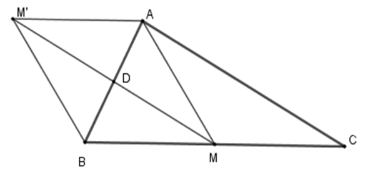
Vì \(M'\) đối xứng $M$ qua $D$ nên \(DM = DM'\) (1).
$M,D$ lần lượt là trung điểm của $BC,AB$ nên $MD$ là đường trung bình của $\Delta ABC$ . Suy ra \(MD{\rm{//}}AC\) (2).
Mặt khác $\Delta ABC$vuông ở $A$ nên \(AB \bot AC\)(2).
Từ (1) và (2) suy ra \(DM \bot AB \Rightarrow MM' \bot AB\).
Vì $D$ là trung điểm của $AB$(gt) và $D$ là trung điểm của \(MM'\) nên tứ giác $AMBM'$là hình bình hành. Mặt khác \(MM' \bot AB\)nên $AMBM'$ là hình thoi.
Cho tam giác $ABC$ vuông ở \(A\) , trung tuyến $AM$ . Gọi $D$ là trung điểm của $AB$ , $M'$ là điểm đối xứng với $M$ qua $D$ .
Cho \(BC = 4\,cm\) . Tính chu vi tứ giác \(AMBM'\).
Vì \(BC = 4\,cm\) nên \(BM = \dfrac{{BC}}{2} = 2\,cm\) .
Chu vi tứ giác $AMBM'$ bằng \(4.BM = 4.2 = 8\,cm\).
Cho tứ giác $ABCD$ . Gọi $E,F,G$$,H$ lần lượt là trung điểm của $AB,BC,CD,DA$ . Các đường chéo $AC,BD$ của tứ giác $ABCD$ phải có điều kiện gì thì $EFGH$ là hình thoi?
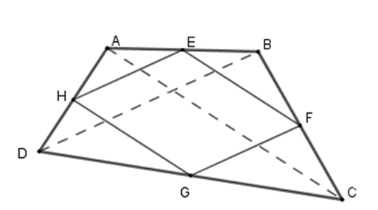
Vì $E,F$ lần lượt là trung điểm của$AB$ , $BC$ nên $EF$ là đường trung bình của $\Delta ABC$ . Suy ra \(EF{\rm{//}}AC\) và \(EF = \dfrac{1}{2}AC\) (1).
Tương tự ta có : \(HG{\rm{//}}AC\) và \(HG = \dfrac{1}{2}AC\) (2).
Từ (1) và (2) suy ra tứ giác $EFGH$ là hình bình hành.
Muốn cho tứ giác $EFGH$ là hình thoi thì nó cần phải có thêm hai cạnh kề bằng nhau.
Nên \(EH = EF \Leftrightarrow AC = BD\).
Cho tam giác $ABC$ . Trên các cạnh $AB$ và $AC$ lần lượt lấy hai điểm $D$ và $E$ sao cho $BD = CE$ . Gọi $M,N,P,Q$ thứ tự là trung điểm của $BE,CD,DE$ và $BC$ . Chọn câu đúng nhất.
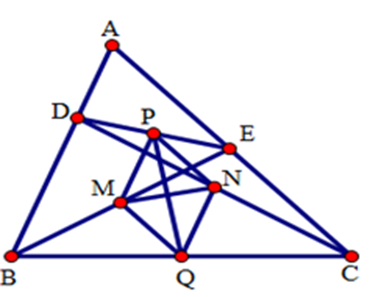
Từ giả thiết ta có $MP,NP,NQ,QM$ lần lượt là các đường trung bình của các tam giác $BDE,ECD,DCB,BEC$ . (định nghĩa đường trung bình).
Đặt $BD = CE = 2a$ .
Áp dụng định lý đường trung bình và giả thiết vào bốn tam giác trên ta được:
\(MP = \dfrac{1}{2}BD = a;NQ = \dfrac{1}{2}DB = a;\)\(NP = \dfrac{1}{2}CE = a;MQ = \dfrac{1}{2}CE = a.\)
Suy ra $MN = NP = PQ = QM$ .
Tứ giác $MNPQ$ có bốn cạnh bằng nhau nên là hình thoi.
Áp dụng tính chất về đường chéo vào hình thoi $MNPQ$ ta được: \(MN \bot PQ\).
Cho hình thoi $ABCD$ có góc $A$ tù. Biết đường cao kẻ từ đỉnh $A$ đến cạnh $CD$ chia đôi cạnh đó. Tính các góc của hình thoi.
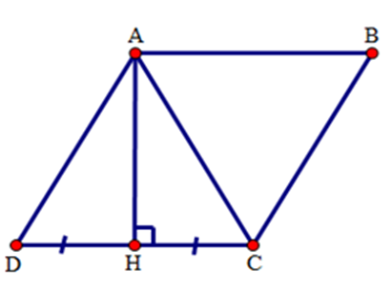
Gọi $H$ là chân đường cao kẻ từ $A$ đến cạnh $CD$ . Từ giả thiết ta có: \(AH \bot DC,CH = HD\) suy ra $AH$ là đường trung trục của đoạn $CD$ nên $AC = CD$ . (1)
Do $ABCD$ là hình thoi nên $AD = CD$ (2)
Từ (1) và (2) suy ra $AD = CD = AC$ nên tam giác $ACD$ là tam giác đều, do đó \(\widehat D = {60^0}\) .
Vì góc $A$ và góc $D$ là hai góc trong cùng phía của $AB$ // $CD$ nên chúng bù nhau hay \(\widehat A = {180^0} - {60^0} = {120^0}\).
Áp dụng tính chất về góc vào hình thoi ta được: $\widehat B = \widehat D = {60^0},\,\,\widehat A = \widehat C = {120^0}$.
Cho tam giác ABC đều, H là trực tâm, đường cao AD. M là điểm bất kì trên trên cạnh BC. Gọi E, F lần lượt là hình chiếu của M trên AB, AC, gọi I là trung điểm của đoạn thẳng AM. ID cắt EF tại K.
Chọn câu sai.
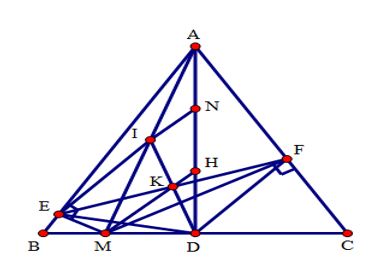
Tam giác EAM vuông tại E, EI là đường trung tuyến nên: \(EI = IM = IA = \dfrac{1}{2}AM\).
Từ EI = IA suy ra tam giác IAE cân tại I, từ đó có: \(\widehat {EIM} = 2\widehat {EAI}\) (góc ngoài của tam giác).
Chứng minh tương tự với tam giác vuông \(ADM\) ta có: \(\widehat {MID} = 2\widehat {IAD},DI = \dfrac{1}{2}AM\).
Do đó:
\(EI = DI\,\,\left( { = \dfrac{1}{2}AM} \right);\,\,\,\widehat {EID} = \widehat {EIM} + \widehat {MID} = 2\left( {\widehat {EAI} + \widehat {IAD}} \right) = 2\widehat {EAD} = {60^0}\).
Tam giác IED cân (vì EI = DI) có: \(\widehat {EID} = {60^0}\) nên là tam giác đều, từ đó EI = ED = ID.
Tương tự tam giác IDF đều suy ra: \(ID = DF = IF.\)
Do đó \(EI = ED = DF = IF.\) Suy ra tứ giác EIFD là hình thoi.
Suy ra K là trung điểm chung của EF và ID.
Gọi N là trung điểm của AH.
Tam giác ABC đều có H là trực tâm của tam giác ABC nên H cũng là trọng tâm tam giác.
Do đó \(AN = NH = HD.\)
Ta có: \(MH//IN\) (vì IN là đường trung bình của tam giác AMH) và \(KH//IN\) (vì KH là đường trung bình của tam giác DIN).
Từ H ta chỉ vẽ được một đường thẳng song song với IN (tiên đề Ơ – Clit) nên M, H, K thẳng hàng.
Vậy D sai vì \(ID = IF\)

