Câu hỏi:
2 năm trước
Cho tam giác $ABC$ vuông ở \(A\) , trung tuyến $AM$ . Gọi $D$ là trung điểm của $AB$ , $M'$ là điểm đối xứng với $M$ qua $D$ .
Tứ giác \(AMBM'\) là hình gì?
Trả lời bởi giáo viên
Đáp án đúng: a
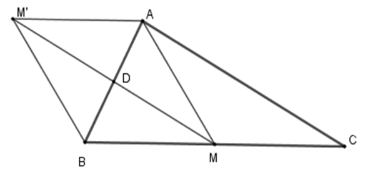
Vì \(M'\) đối xứng $M$ qua $D$ nên \(DM = DM'\) (1).
$M,D$ lần lượt là trung điểm của $BC,AB$ nên $MD$ là đường trung bình của $\Delta ABC$ . Suy ra \(MD{\rm{//}}AC\) (2).
Mặt khác $\Delta ABC$vuông ở $A$ nên \(AB \bot AC\)(2).
Từ (1) và (2) suy ra \(DM \bot AB \Rightarrow MM' \bot AB\).
Vì $D$ là trung điểm của $AB$(gt) và $D$ là trung điểm của \(MM'\) nên tứ giác $AMBM'$là hình bình hành. Mặt khác \(MM' \bot AB\)nên $AMBM'$ là hình thoi.
Hướng dẫn giải:
Bước 1: Chứng minh \(MM' \bot AB\) .
Bước 2: Dùng dấu hiệu nhận biết: “Tứ giác có hai đường chéo giao nhau tại trung điểm mỗi đường và vuông góc với nhau là hình thoi” để chứng minh \(AMBM'\) là hình thoi.
