Câu hỏi:
2 năm trước
Cho tứ giác $ABCD$ . Gọi $E,F,G$$,H$ lần lượt là trung điểm của $AB,BC,CD,DA$ . Các đường chéo $AC,BD$ của tứ giác $ABCD$ phải có điều kiện gì thì $EFGH$ là hình thoi?
Trả lời bởi giáo viên
Đáp án đúng: a
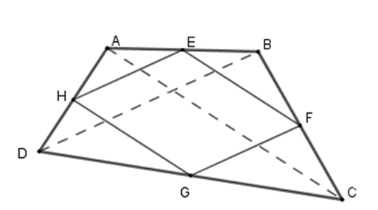
Vì $E,F$ lần lượt là trung điểm của$AB$ , $BC$ nên $EF$ là đường trung bình của $\Delta ABC$ . Suy ra \(EF{\rm{//}}AC\) và \(EF = \dfrac{1}{2}AC\) (1).
Tương tự ta có : \(HG{\rm{//}}AC\) và \(HG = \dfrac{1}{2}AC\) (2).
Từ (1) và (2) suy ra tứ giác $EFGH$ là hình bình hành.
Muốn cho tứ giác $EFGH$ là hình thoi thì nó cần phải có thêm hai cạnh kề bằng nhau.
Nên \(EH = EF \Leftrightarrow AC = BD\).
Hướng dẫn giải:
Sử dụng dấu hiệu nhận biết hình thoi