Cho tam giác ABC đều, H là trực tâm, đường cao AD. M là điểm bất kì trên trên cạnh BC. Gọi E, F lần lượt là hình chiếu của M trên AB, AC, gọi I là trung điểm của đoạn thẳng AM. ID cắt EF tại K.

Chọn câu sai.

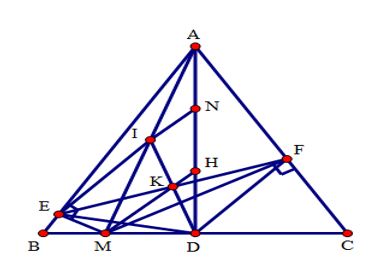
Tam giác EAM vuông tại E, EI là đường trung tuyến nên: \(EI = IM = IA = \dfrac{1}{2}AM\).

Từ EI = IA suy ra tam giác IAE cân tại I, từ đó có: \(\widehat {EIM} = 2\widehat {EAI}\) (góc ngoài của tam giác).

Chứng minh tương tự với tam giác vuông \(ADM\) ta có: \(\widehat {MID} = 2\widehat {IAD},DI = \dfrac{1}{2}AM\).

Do đó:

\(EI = DI\,\,\left( { = \dfrac{1}{2}AM} \right);\,\,\,\widehat {EID} = \widehat {EIM} + \widehat {MID} = 2\left( {\widehat {EAI} + \widehat {IAD}} \right) = 2\widehat {EAD} = {60^0}\).

Tam giác IED cân (vì EI = DI) có: \(\widehat {EID} = {60^0}\) nên là tam giác đều, từ đó EI = ED = ID.

Tương tự tam giác IDF đều suy ra: \(ID = DF = IF.\)

Do đó \(EI = ED = DF = IF.\) Suy ra tứ giác EIFD là hình thoi.

Suy ra K là trung điểm chung của EF và ID.

Gọi N là trung điểm của AH.

Tam giác ABC đều có H là trực tâm của tam giác ABC nên H cũng là trọng tâm tam giác.

Do đó \(AN = NH = HD.\)

Ta có: \(MH//IN\) (vì IN là đường trung bình của tam giác AMH) và \(KH//IN\) (vì KH là đường trung bình của tam giác DIN).

Từ H ta chỉ vẽ được một đường thẳng song song với IN (tiên đề Ơ – Clit) nên M, H, K thẳng hàng.

Vậy D  sai vì \(ID = IF\)