Đề thi khảo sát chất lượng đầu năm - Đề số 4

Xét tam giác \(\Delta ABC\) có: \(\widehat {BAC} = {60^0}\), \(\widehat {BCA} = {30^0}\) ta có: \(\widehat {BAC} + \widehat {BCA} + \widehat {CBA} = {180^0}\).

Suy ra: \(\widehat {CBA} = {180^0} - \widehat {BAC} - \widehat {CBA}\) \( = {180^0} - {60^0} - {30^0} = {90^0}\).

Do đó \(\widehat {CBA} > \widehat {BAC} > \widehat {BCA}\) \(\left( {{{90}^0} > {{60}^0} > {{30}^0}} \right)\) nên \(AC > BC > AB\) (đối diện với góc lớn hơn là cạnh lớn hơn).

Ta có:

\(\begin{array}{l}P\left( x \right)\,\,\, = 1 + 3{x^4} + 2{x^2} + {x^4} + {x^3} + 5{x^2} + 3{x^3}\\\, = \left( {3{x^4} + {x^4}} \right) + \left( {{x^3} + 3{x^3}} \right) + \left( {2{x^2} + 5{x^2}} \right) + 1\,\\ = \,4{x^4} + 4{x^3} + 7{x^2} + 1\,\end{array}\)

\(\begin{array}{l}Q\left( x \right) =  - 4{x^4} - 2{x^2} - 4{x^3} + 2x - 4{x^2} - x - \dfrac{1}{4}\\ =  - 4{x^4} - 4{x^3} + \left( { - 2{x^2} - 4{x^2}} \right) + \left( {2x - x} \right) - \dfrac{1}{4}\\ = \, - 4{x^4} - 4{x^3} - 6{x^2} + x - \dfrac{1}{4}\end{array}\)

Vậy \(P\left( x \right) = \,4{x^4} + 4{x^3} + 7{x^2} + 1\,;\)\(Q\left( x \right) = \, - 4{x^4} - 4{x^3} - 6{x^2} + x - \dfrac{1}{4}.\)

Theo câu trước ta có: \(P\left( x \right) = \,4{x^4} + 4{x^3} + 7{x^2} + 1\,;\) \(Q\left( x \right) = \, - 4{x^4} - 4{x^3} - 6{x^2} + x - \dfrac{1}{4}.\)

Suy ra:

\( + )\,P\left( x \right) + Q\left( x \right) = \left( {4{x^4} - 4{x^4}} \right) + \left( {4{x^3} - 4{x^3}} \right) + \left( {7{x^2} - 6{x^2}} \right) + x - \dfrac{1}{4} + 1\)\( \Leftrightarrow \,P\left( x \right) + Q\left( x \right) = \,{x^2} + x + \dfrac{3}{4}\)

\( + )P\left( x \right) - Q\left( x \right) = \left( {4{x^4} - \left( { - 4{x^4}} \right)} \right) + \left( {4{x^3} - \left( { - 4{x^3}} \right)} \right) + \left( {7{x^2} - \left( { - 6{x^2}} \right)} \right) - x + \dfrac{1}{4} + 1\)\( \Leftrightarrow P\left( x \right) - Q\left( x \right)\, = 8{x^4} + 8{x^3} + 13{x^2} - x + \dfrac{5}{4}\).

Vậy \(\,P\left( x \right) + Q\left( x \right) = \,{x^2} + x + \dfrac{3}{4};\)\(P\left( x \right) - Q\left( x \right)\, = 8{x^4} + 8{x^3} + 13{x^2} - x + \dfrac{5}{4}\).

Sử dụng kết quả câu trước \(\,P\left( x \right) + Q\left( x \right) = \,{x^2} + x + \dfrac{3}{4}\).

Xét: \(P\left( x \right) + Q\left( x \right) = 0\)

\(\begin{array}{l} \Leftrightarrow \,{x^2} + x + \dfrac{3}{4} = \left( {{x^2} + 2.\dfrac{1}{2}.x + \dfrac{1}{4}} \right) + \dfrac{2}{4}\\ = {\left( {x + \dfrac{1}{2}} \right)^2} + \dfrac{1}{2} \ge \dfrac{1}{2}\,\,\,\,\,\,\forall x\end{array}\).

Vậy \(P\left( x \right) + Q\left( x \right)\) luôn không có nghiệm.

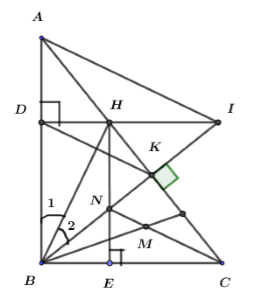
\(\Delta BHK = \Delta BHD\)

Vì BK là đường cao của tam giác \(\Delta ABC\) nên \(BK \bot AC\)

Xét hai tam giác vuông \(BHK\) và \(\Delta BHD\) ta có:

\(\angle {B_1} = \angle {B_2}\) (do BH là đường phân giác của góc \(\angle ABK\left( {H \in AC} \right).\)

Cạnh BH chung

\( \Rightarrow \Delta BHK = \Delta BHD\) (cạnh huyền-góc nhọn)

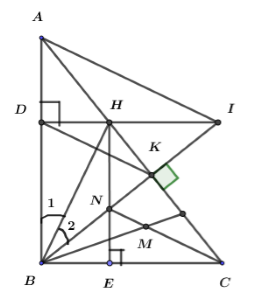
+) Vì \(\Delta BHK = \Delta BHD\) nên \(HK = HD\) (cạnh tương ứng)

Xét hai tam giác \(\Delta ADH;\,\Delta IKH\)

Có:

+) \(\angle DHA = \angle KHI\) (đối đỉnh)

+) \(HK = HD\)(cmt)

+) \(\angle ADH = \angle IKH = {90^0}\)

\( \Rightarrow \Delta ADH = \,\,\Delta IKH\) (g.c.g)

\(IK = AD\) (cạnh tương ứng)

+) Trong tam giác \(ABC\) có:

\(\begin{array}{l}AB = AD + DB\\BI = BK + KI\end{array}\)

Mà \(AD = IK\,\) (do \(\Delta ADH = \Delta IKH\left( {cmt} \right)\))

\(DB = BK\) (do \(\Delta BHK = \Delta BHD\))

\( \Rightarrow AB = BI\)

\( \Rightarrow \Delta ABI\) là tam giác cân tại B. \( \Rightarrow \angle BAI = \angle BIA\)

Trong một tam giác cân, tia phân giác ứng với cạnh đáy chính là đường cao

\( \Rightarrow BH \bot AI\,\,\left( 1 \right)\)

Mà \(\Delta BDK\) cũng cân tại B (do \(BD = BK\left( {do\,\Delta BDH = \Delta BKH} \right)\)

\( \Rightarrow BH \bot DK\,\,\left( 2 \right)\) (do BH là đường phân giác góc B)

Từ (1) và (2) \( \Rightarrow DK//AI\) (do cùng vuông góc với \(BH\))  

Vậy \(DK//AI\).

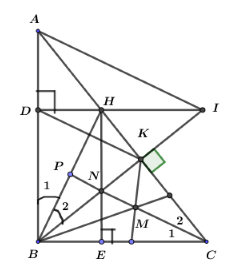
Xét tam giác \(HBC\) ta có:

\(BK \bot HC\left( {Gt} \right) \Rightarrow BK\) là đường cao xuất phát từ đỉnh \(B\) của tam giác \(HBC\).

Ta có:

\(\begin{array}{l}DI \bot AB\left( {GT} \right)\\BC \bot AB\left( {gt} \right)\,\,\,\,\,\, \Rightarrow \angle DIB = \angle KBC\,\left( {so\,le\,trong} \right)\\ \Rightarrow DI//BC\end{array}\)

Mà:

\(\begin{array}{l}\angle C + \angle KBC = {90^0}\\\angle DBI + \angle DIB = {90^0}\\ \Rightarrow \angle C = \angle DBI\\ \Rightarrow \angle {B_1} = \angle {B_2} = \angle {C_1} = \angle {C_2}\,\,\,\left( 1 \right)\end{array}\)

Kéo dài CN cắt BH tại P, ta chứng minh CP là đường cao kẻ từ đỉnh C của tam giác \(HBC\).

Ta có:

\(\begin{array}{l} + )\,\angle C + \angle KBC = {90^0}\\ + )\angle {C_1} + \angle {C_2} + \angle KBC = {90^0}\end{array}\).

Mà \(\angle {C_2} = \angle {B_2}\,\,\left( {cmt} \right) \Rightarrow \angle {C_1} + \angle KBC + \angle {B_2} = \angle BPC = {90^0}\) Hay \(CP \bot CH\).

Trong tam giác \(HBC\) có: CN là đường cao, BN là đường cao.

\( \Rightarrow \) N là trực tâm của \(\Delta HBC\).

\(\begin{array}{l}B = \left( { - 2\dfrac{1}{3}{x^2}{y^2}} \right).\dfrac{9}{{16}}x{y^2}.{\left( { - 2{x^2}y} \right)^3}\\\,\,\,\, = \left( { - 2\dfrac{1}{3}.\dfrac{9}{{16}}.{{\left( { - 2} \right)}^3}} \right){x^2}{y^2}.x{y^2}.{\left( {{x^2}y} \right)^3}\\\,\,\,\, = \,\dfrac{{ - 7}}{3}.\dfrac{9}{{16}}.\left( { - 8} \right).{x^9}{y^7}\\\,\,\,\, = \dfrac{{21}}{2}.{x^9}.{y^7}\end{array}\).

Tổng các số mũ của các biến là: \(9 + 7 = 16\)

\( \Rightarrow \) đơn thức có bậc bằng 16.

Vậy \(B = \dfrac{{21}}{2}{x^9}{y^7}\), hệ số: \(\dfrac{{21}}{2}\) và có bậc \(16.\)

Ta có: \(4{x^2} + 2{y^2} + 4{z^2} - 4xy--4y + 4z\; + 5 = 0\)

\( \Leftrightarrow \left( {4{x^2} - 4xy + {y^2}} \right) + \left( {{y^2} - 4y + 4} \right) + \left( {4{z^2} + 4z + 1} \right) = 0\)

\( \Leftrightarrow {\left( {2x--y} \right)^2} + {\left( {y-2{\rm{ }}} \right)^2} + {\left( {2z + 1} \right)^2} = 0\)  (*)

Mà \({\left( {2x - y} \right)^2} \ge 0;{\left( {y - 2} \right)^2} \ge 0;{\left( {2z + 1} \right)^2} \ge 0\) với mọi \(x;y;z\). Nên từ (*) suy ra:

\(\left\{ \begin{array}{l}{\left( {2x - y} \right)^2} = 0\\{\left( {y - 2} \right)^2} = 0\\{\left( {2z + 1} \right)^2} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - y = 0\\y - 2 = 0\\2z + 1 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{y}{2}\\y = 2\\z =  - \dfrac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\\z =  - \dfrac{1}{2}\end{array} \right.\)

Suy ra: \(x + y + z = 1 + 2 + \left( { - \dfrac{1}{2}} \right) = \dfrac{5}{2}\).