Cho \(\Delta ABC\) vuông tại \(B\), đường cao \(BK\left( {K \in AC} \right).\) Vẽ \(BH\) là tia phân giác của \(\angle ABK\left( {H \in AC} \right).\) Kẻ \(HD\) vuông góc với \(AB.\) Gọi giao điểm của \(DH\) và \(BK\) là \(I\). Các đường phân giác của \(\Delta BKC\) cắt nhau tại \(M\). Gọi \({\rm N}\) là giao điểm của \(CM\,\)và \(BK\).
Chọn câu đúng.
Trả lời bởi giáo viên
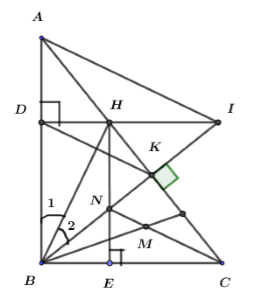
\(\Delta BHK = \Delta BHD\)
Vì BK là đường cao của tam giác \(\Delta ABC\) nên \(BK \bot AC\)
Xét hai tam giác vuông \(BHK\) và \(\Delta BHD\) ta có:
\(\angle {B_1} = \angle {B_2}\) (do BH là đường phân giác của góc \(\angle ABK\left( {H \in AC} \right).\)
Cạnh BH chung
\( \Rightarrow \Delta BHK = \Delta BHD\) (cạnh huyền-góc nhọn)
Hướng dẫn giải:
Chứng minh hai tam giác vuông bằng nhau theo trường hợp cạnh huyền góc nhọn, bằng cách chỉ ra hai cạnh huyền tương ứng bằng nhau, hai góc nhọn tương ứng bằng nhau.

