Trả lời bởi giáo viên
Đáp án đúng: c
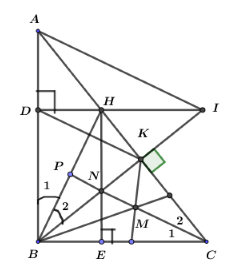
Xét tam giác \(HBC\) ta có:
\(BK \bot HC\left( {Gt} \right) \Rightarrow BK\) là đường cao xuất phát từ đỉnh \(B\) của tam giác \(HBC\).
Ta có:
\(\begin{array}{l}DI \bot AB\left( {GT} \right)\\BC \bot AB\left( {gt} \right)\,\,\,\,\,\, \Rightarrow \angle DIB = \angle KBC\,\left( {so\,le\,trong} \right)\\ \Rightarrow DI//BC\end{array}\)
Mà:
\(\begin{array}{l}\angle C + \angle KBC = {90^0}\\\angle DBI + \angle DIB = {90^0}\\ \Rightarrow \angle C = \angle DBI\\ \Rightarrow \angle {B_1} = \angle {B_2} = \angle {C_1} = \angle {C_2}\,\,\,\left( 1 \right)\end{array}\)
Kéo dài CN cắt BH tại P, ta chứng minh CP là đường cao kẻ từ đỉnh C của tam giác \(HBC\).
Ta có:
\(\begin{array}{l} + )\,\angle C + \angle KBC = {90^0}\\ + )\angle {C_1} + \angle {C_2} + \angle KBC = {90^0}\end{array}\).
Mà \(\angle {C_2} = \angle {B_2}\,\,\left( {cmt} \right) \Rightarrow \angle {C_1} + \angle KBC + \angle {B_2} = \angle BPC = {90^0}\) Hay \(CP \bot CH\).
Trong tam giác \(HBC\) có: CN là đường cao, BN là đường cao.
\( \Rightarrow \) N là trực tâm của \(\Delta HBC\).
Hướng dẫn giải:
Nhớ lại kiến thức về các đường đồng quy trong tam giác.
Ta chứng minh hai đường cao của tam giác HBC cắt nhau tại N.
Câu hỏi khác
- Đề thi khảo sát chất lượng đầu năm - Đề số 1 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 2 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 3 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 5 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 4 toán 8 có lời giải
