Trả lời bởi giáo viên
Đáp án đúng: d
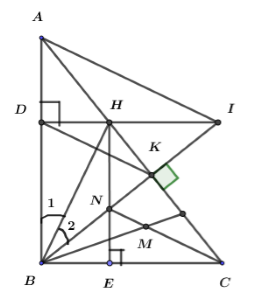
+) Vì \(\Delta BHK = \Delta BHD\) nên \(HK = HD\) (cạnh tương ứng)
Xét hai tam giác \(\Delta ADH;\,\Delta IKH\)
Có:
+) \(\angle DHA = \angle KHI\) (đối đỉnh)
+) \(HK = HD\)(cmt)
+) \(\angle ADH = \angle IKH = {90^0}\)
\( \Rightarrow \Delta ADH = \,\,\Delta IKH\) (g.c.g)
\(IK = AD\) (cạnh tương ứng)
+) Trong tam giác \(ABC\) có:
\(\begin{array}{l}AB = AD + DB\\BI = BK + KI\end{array}\)
Mà \(AD = IK\,\) (do \(\Delta ADH = \Delta IKH\left( {cmt} \right)\))
\(DB = BK\) (do \(\Delta BHK = \Delta BHD\))
\( \Rightarrow AB = BI\)
\( \Rightarrow \Delta ABI\) là tam giác cân tại B. \( \Rightarrow \angle BAI = \angle BIA\)
Trong một tam giác cân, tia phân giác ứng với cạnh đáy chính là đường cao
\( \Rightarrow BH \bot AI\,\,\left( 1 \right)\)
Mà \(\Delta BDK\) cũng cân tại B (do \(BD = BK\left( {do\,\Delta BDH = \Delta BKH} \right)\)
\( \Rightarrow BH \bot DK\,\,\left( 2 \right)\) (do BH là đường phân giác góc B)
Từ (1) và (2) \( \Rightarrow DK//AI\) (do cùng vuông góc với \(BH\))
Vậy \(DK//AI\).
Hướng dẫn giải:
+) Xét hai tam giác \(\Delta ADH;\,\,\,\,\,\Delta IKH\) chứng minh hai tam giác này bằng nhau, rồi suy ra hai cạnh tương ứng bằng nhau.
+) Chứng minh \(DK;\,AI\) cùng vuông góc với \(BH\).
Câu hỏi khác
- Đề thi khảo sát chất lượng đầu năm - Đề số 1 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 2 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 3 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 5 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 4 toán 8 có lời giải
