Câu hỏi:
2 năm trước
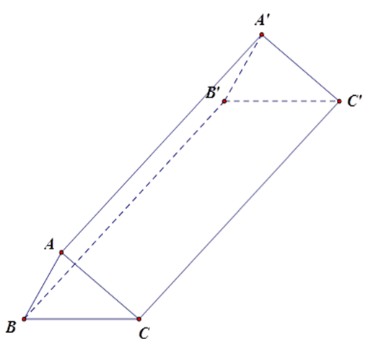
Một hình lăng trụ đứng có đáy là hình thoi với các đường chéo của đáy bằng \(24\,cm\) và \(10\,cm\). Diện tích toàn phần của hình lăng trụ bằng \(1020\)\(c{m^2}\). Tính chiều cao của hình lăng trụ.
Trả lời bởi giáo viên
Đáp án đúng: a
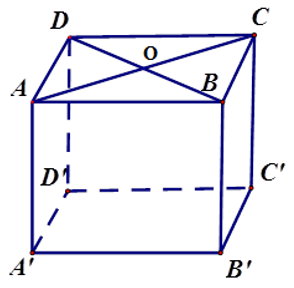
Vì đáy \(ABCD\) là hình thoi nên diện tích đáy bằng: \(24.10:2 = 120\,(c{m^2})\)
Từ đó diện tích xung quanh: \({S_{xq}} = 1020 - 120.2 = 780\,(c{m^2})\)
Vì \(ABCD\) là hình thoi nên \(AB \bot CD;\,OD = \dfrac{{BD}}{2} = \dfrac{{24}}{2} = 12\,cm\); \(OA = \dfrac{{AC}}{2} = \dfrac{{10}}{2} = 5\,cm\).
Nên độ dài cạnh đáy bằng \(AD = \sqrt {O{A^2} + O{D^2}} = \sqrt {{5^2} + {{12}^2}} = 13\,(cm)\) (định lý Pytago)
Chu vi đáy bằng: \(13.4 = 52\,(cm)\)
Chiều cao hình lăng trụ bằng:
\(780:52 = 15\,(cm)\).
Hướng dẫn giải:
Sử dụng công thức tính diện tích toàn phần, diện tích xung quanh của hình lăng trụ để suy ra chiều cao của lăng trụ.
