Câu hỏi:
2 năm trước
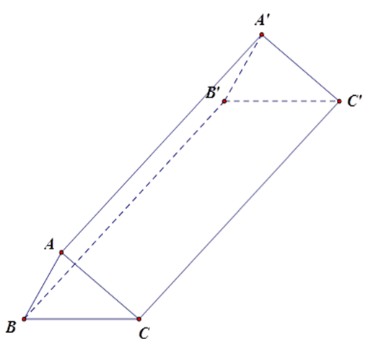
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có \(AB = 5cm,AC = 12cm,BC = 13cm\). Mặt phẳng nào dưới đây không vuông góc với mặt phẳng \(\left( {ABB'A'} \right)\)?
Trả lời bởi giáo viên
Đáp án đúng: a
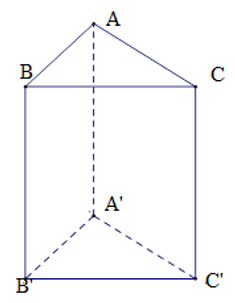
Tam giác \(ABC\) có: \(A{B^2} + A{C^2} = {5^2} + {12^2} = {13^2} = B{C^2}\) nên \(\Delta ABC\) vuông tại \(A\) (định lý Pytago đảo)
nên \(AC \bot AB\). Do đó \(A'C' \bot A'B'\).
Vì \(AC\) vuông góc với hai đường thẳng cắt nhau \(AB\) và \(AA'\) nên \(AC \bot mp \,(ABB'A')\) do đó \(mp \,(A'B'C') \bot mp\,(ABB'A')\).
Vậy có ba mặt phẳng vuông góc với mặt phẳng \(\left( {ABB'A'} \right)\) là mp \(\left( {ABC} \right)\), mp \(\left( {A'B'C'} \right)\), mp \(\left( {ACC'A'} \right).\)
Hướng dẫn giải:
+ Dùng định lý Pytago đảo để chứng minh tam giác vuông.
+ Dùng quan hệ vuông góc giữa hai mặt phẳng để tìm các cặp mặt phẳng vuông góc.
