Một hình hộp chữ nhật có đường chéo bằng \(3\,dm\), chiều cao \(2\,dm\), diện tích xung quanh bằng \(12\)\(d{m^2}\). Diện tích toàn phần của hình hộp chữ nhật là:

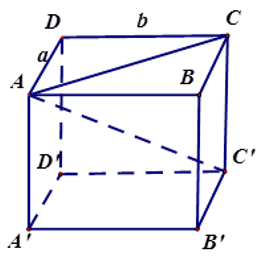
Hình hộp chữ nhật \(ABCD.A'B'C'D'\) có: \(AC' = 3\,dm;\,AC = 2\,dm\).

Xét tam giác \(ACC'\) vuông tại \(C\), theo định lý Pytago ta có: \(A{C^2} = C'{A^2} - C'{C^2} = {3^2} - {2^2} = 5\).

Vì diện tích xung quanh là \(12\,d{m^2}\) nên chu vi đáy bằng \(12:2 = 6\left( {dm} \right)\)

Đặt \(AD = a,{\rm{ }}DC = b\)

Vì chu vi đáy là \(6\,dm \Rightarrow \) \(2\left( {a + b} \right) = 6 \Leftrightarrow a + b = 3\) (1) và \({a^2} + {b^2} = A{C^2} = 5\) (2)

(định lý Pyatgo cho tam giác vuông\(ADC\)) 

Từ (1) và (2) suy ra \({a^2} + (3 - {a^2}) = 5\)

Rút gọn được \({a^2} - 3a + 2 = 0\) hay \((a - 1)(a - 2) = 0\)

Giả sử \(a \ge b\) thì ta tìm được: a = 2 suy ra b = 1.

Diện tích toàn phần của hình hộp chữ nhật bằng: \(12 + 2.1.2 = 16\,(d{m^3})\).