Câu hỏi:
3 năm trước
Tính thể tích của hình lăng trụ đứng có chiều cao \(20\,{\rm{cm}}\), đáy là một tam giác cân có cạnh bên bằng \(5{\rm{cm}}\) và cạnh đáy bằng \(8\,{\rm{cm}}\).
Trả lời bởi giáo viên
Đáp án đúng: d
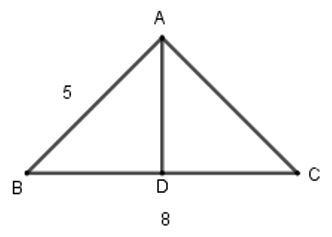
Gọi \(D\) là trung điểm của \(BC\) thì \(AD\) là trung tuyến cũng là đường cao trong tam giác \( \Rightarrow DB = DC = \dfrac{8}{2} = 4\left( {cm} \right)\) và \(AD \bot BC\).
Tam giác \(ADC\) vuông tại \(D\) nên \(A{D^2} + D{C^2} = A{C^2} \Leftrightarrow A{D^2} + {4^2} = {5^2}\)\( \Leftrightarrow A{D^2} = 9 \Leftrightarrow AD = 3\)
Diện tích đáy: \(S = \dfrac{{3.8}}{2} = 12\,\left( {c{m^2}} \right)\).
Thể tích lăng trụ đứng là: \(V = S.h = 12.20 = 240\,c{m^3}\).
Hướng dẫn giải:
Sử dụng công thức tính thể tích hình lăng trụ đứng \(V = S.h\) với \(S\) là diện tích đáy, \(h\) là chiều cao.