Trả lời bởi giáo viên
Đáp án đúng: d
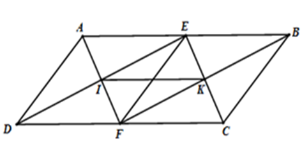
Ta có $EIFK$ là hình chữ nhật (theo câu trước).
Để hình chữ nhật $EIFK$ là hình vuông $ \Leftrightarrow IE = {\rm{IF}}\left( 1 \right)$.
Mà \(I\) là giao điểm hai đường chéo \(DE;AF\) của hình thoi\(AEFD\) nên $IE = \dfrac{1}{2}DE;{\rm{IF = }}\dfrac{1}{2}{\rm{AF}} \Rightarrow {\rm{DE = AF}}$
Mặt khác ta có $AEFD$ là hình thoi (chứng minh ở câu trước) (2).
Từ (1) và (2) $ \Rightarrow AEFD$ là hình vuông $ \Rightarrow AD \bot DC$.
Suy ra hình bình hành \(ABCD\) phải là hình chữ nhật thì \(EIFK\) là hình vuông.
Hướng dẫn giải:
Dựa vào dấu hiệu nhận biết: Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông để suy ra điều kiện của hình bình hành \(ABCD.\)

