Tính \(\dfrac{3}{4}. 26\dfrac{1}{5} - \dfrac{3}{4}. 44\dfrac{1}{5}\).
Ta có:
\(\begin{array}{l}\dfrac{3}{4}. 26\dfrac{1}{5} - \dfrac{3}{4}. 44\dfrac{1}{5}\\ = \dfrac{3}{4}\left( {26\dfrac{1}{5} - 44\dfrac{1}{5}} \right)\\ = \dfrac{3}{4} \cdot \left( { - 18} \right) = \dfrac{{ - 27}}{2}\end{array}\).
Biết độ dài các cạnh của một tam giác tỉ lệ với \(3,5,7.\) Tính độ dài cạnh lớn nhất của tam giác đó. Biết rằng cạnh lớn nhất dài hơn cạnh nhỏ nhất là \(8{\rm{ }}cm.\)
Gọi độ dài các cạnh của tam giác theo thứ tự tăng dần lần lượt là: \(a,b,c{\rm{ }}\left( {a,b,c > 0} \right)\)
Theo bài ra ta có: \(\dfrac{a}{3} = \dfrac{b}{5} = \dfrac{c}{7}\) và \(c - a = 8.\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{a}{3} = \dfrac{b}{5} = \dfrac{c}{7}\)=\(\dfrac{{c - a}}{{7 - 3}} = \dfrac{8}{4} = 2\).
+) \(a = 2. 3 = 6\)
+) \(b = 2. 5 = 10\)
+) \(c = 2. 7 = 14\)
Vậy: độ dài các cạnh của tam giác lần lượt là: \(6{\rm{ }}cm;10{\rm{ }}cm;14cm.\)
Cho đa thức \(A\left( x \right) = {x^4} - {x^2} + 1\).
Tìm bậc của đa thức trên.
\(A\left( x \right)\) có bậc 4.
Cho đa thức \(A\left( x \right) = {x^4} - {x^2} + 1\).
Tính \(A\left( { - 1} \right);A\left( { - 2} \right).\)
Ta có :
\(\begin{array}{l}A\left( { - 1} \right) = {\left( { - 1} \right)^4} - {\left( { - 1} \right)^2} + 1 = 1\\A\left( { - 2} \right) = \,{\left( { - 2} \right)^4} - {\left( { - 2} \right)^2} + 1 = 13\end{array}\).
Cho đa thức \(A\left( x \right) = {x^4} - {x^2} + 1\).
Tìm nghiệm của đa thức \(Q\left( x \right) = 2{x^2} + x\).
Ta có:
\(\begin{array}{l}2{x^2} + x = 0\\x\left( {2x + 1} \right) = 0\end{array}\)
\( \Rightarrow x = 0\) hoặc \(x = - \dfrac{1}{2}\)
Vậy \(Q\left( x \right)\) có nghiệm là \(x = 0;\,x = - \dfrac{1}{2}\).
Cho tam giác \(ABC\) cân tại \(A\) và hai đường trung tuyến \(BM,\,CN\) cắt nhau tại \(K\).
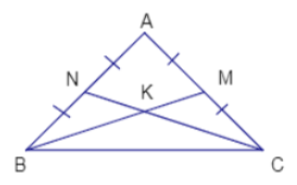
Chọn câu đúng.
Xét \(\Delta BNC\) và \(\Delta CMB\) có:
\(\begin{array}{l}BN = AN = \dfrac{{AB}}{2};\,\\CM = AM = \dfrac{{AC}}{2}\end{array}\)
Mà \(AB = AC\) \( \Rightarrow BN = CM\)
Lại có:
+) \(\widehat B = \widehat C\) (do \(\Delta ABC\) cân tại A)
+) \(BC\) cạnh chung.
Do đó: \(\Delta BNC = \Delta CMB \left( {c.g.c} \right)\).
Cho tam giác \(ABC\) cân tại \(A\) và hai đường trung tuyến \(BM,\,CN\) cắt nhau tại \(K\).

Tam giác\(\,\Delta BKC\) là tam giác.
Theo câu trước ta có: \(\Delta BNC = \Delta CMB\)
Do \(\Delta BNC = \Delta CMB\)
\( \Rightarrow \widehat {MBC} = \widehat {NCB}\) (hai góc tương ứng)
\( \Rightarrow \Delta KBC\) cân tại \(K.\)
Cho tam giác \(ABC\) cân tại \(A\) và hai đường trung tuyến \(BM,\,CN\) cắt nhau tại \(K\).

Chọn câu đúng.
Ta có: \(\Delta KBC\) cân tại \(K\) (theo câu trước)
\( \Rightarrow BK = CK\)
Ta có: \(BK + CK = BK + BK = 2BK = 2.2KM = 4KM\) (tính chất đường trung tuyến).
Mà \(\Delta KBC\) có: \(KB + KC > BC\) (bất đẳng thức tam giác)
Suy ra: \(BC < 4.KM\)
Biết \(\dfrac{{bz - cy}}{a} = \dfrac{{cx - az}}{b} = \dfrac{{ay - bx}}{c}\) (với a, b, c \( \ne \)0).
Ta có:
\(\begin{array}{l}\dfrac{{bz - cy}}{a} = \dfrac{{cx - az}}{b} = \dfrac{{ay - bx}}{c}\\ = \dfrac{{abz - acy}}{{{a^2}}} = \dfrac{{bcx - abz}}{{{b^2}}} \\= \dfrac{{acy - bcx}}{{{c^2}}}\\ = \dfrac{{abz - acy + bcx - abz + acy - bcx}}{{{a^2} + {b^2} + {c^2}}} \\= \dfrac{0}{{{a^2} + {b^2} + {c^2}}} = 0\end{array}\).
Suy ra: \(\dfrac{{bz - cy}}{a} = 0\), do đó \(bz = cy\) hay \(\dfrac{y}{b} = \dfrac{z}{c}(1)\)
\(\dfrac{{cx - az}}{b} = 0\), do đó \(cx = az\) hay \(\dfrac{z}{c} = \dfrac{x}{a}(2)\)
Từ (1) và (2) suy ra: \(\dfrac{a}{x} = \dfrac{b}{y} = \dfrac{c}{z}.\)

