Trả lời bởi giáo viên
Đáp án đúng: a
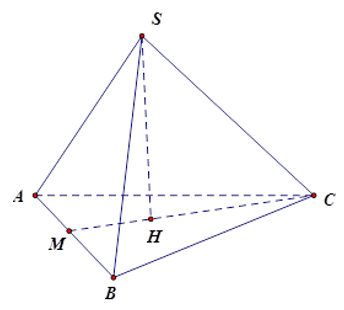
Gọi \(M\) là giao điểm của \(CH\) và \(AB\) ta có: \(CM \bot AB\) và \(AM = MB\).
Vì \(H\) là trọng tâm \(\Delta ABC\) nên \(CM = \dfrac{3}{2}CH = \dfrac{3}{2}.3\sqrt 3 = \dfrac{{9\sqrt 3 }}{2}(cm)\)
Đặt \(AB = BC = x\), ta có: \(B{C^2} - M{B^2} = C{M^2}\) (định lý Pytago cho \(\Delta MBC\)) nên
\({x^2} - {\left( {\dfrac{x}{2}} \right)^2} = {\left( {\dfrac{{9\sqrt 3 }}{2}} \right)^2}\) \( \Leftrightarrow \dfrac{{3{x^2}}}{4} = \dfrac{{243}}{4} \Leftrightarrow {x^2} = 81 \Leftrightarrow x = 9\)
Vậy các cạnh của hình chóp có độ dài là \(9cm\).
Hướng dẫn giải:
Sử dụng định lí Pytago và tính chất trọng tâm tam giác.

