Trả lời bởi giáo viên
Đáp án đúng: d
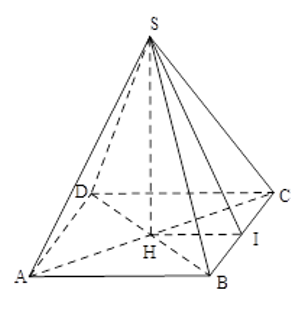
Xét hình chóp tứ giác đều S.ABCD có đường cao
SH=10cm, cạnh AB=48cm
Gọi SI là đường cao của ΔSBC. Tam giác SBC cân tại S nên BI=IC. Ta có: HI là đường trung bình của ΔABCnên HI=AB2=482=24(cm)
Áp dụng định lí Py-ta-go vào tam giác vuông SHI. Ta có: SI2=SH2+HI2=102+242=676=262.
Nên SI=26(cm).
Hướng dẫn giải:
Sử dụng kiến thức về hình chóp đều và định lý Pytago.
