Trả lời bởi giáo viên
Đáp án đúng: d
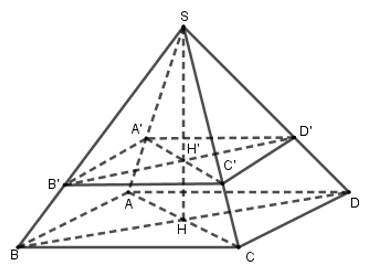
Ta có: \(SH' = \dfrac{2}{3}SH = \dfrac{2}{3}.6 = 4\,cm\)
Xét tam giác \(SAH\) có: \(A'H'//AH\) và \(\dfrac{{SH'}}{{SH}} = \dfrac{2}{3}\) \( \Rightarrow \dfrac{{SA'}}{{SA}} = \dfrac{2}{3}\) (định lí Ta let)
Mà \(A'B'//AB\) \( \Rightarrow \dfrac{{A'B'}}{{AB}} = \dfrac{{SA'}}{{SA}} = \dfrac{2}{3}\) \( \Rightarrow A'B' = \dfrac{2}{3}AB = \dfrac{2}{3}.6 = 4\)
Thể tích hình chóp \(S.A'B'C'D'\) bằng: \(\dfrac{1}{3}{.4^2}.4 = \dfrac{{64}}{3}\,c{m^3}\)
Thể tích hình chóp cụt bằng: \(72 - \dfrac{{64}}{3} = \dfrac{{152}}{3}\,c{m^3}\).
Hướng dẫn giải:
Sử dụng cách tính thể tích hình chóp cụt:
Để tính thể tích của hình chóp cụt đều, ta lấy thể tích của hình chóp đều lớn trừ đi thể tích của hình chóp đều nhỏ.

