Tính diện tích toàn phần của hình chóp tứ giác đều.
Chu vi đáy bằng $24.4 = 96\left( {cm} \right)$
${S_{xq}} = p.d = \dfrac{{96}}{2}.37 = 1776\left( {c{m^2}} \right)$
Diện tích đáy bằng $24.24 = 576\left( {c{m^2}} \right)$
Diện tích toàn phần $1776 + 576 = 2352\left( {c{m^2}} \right)$
Tính độ dài trung đoạn.
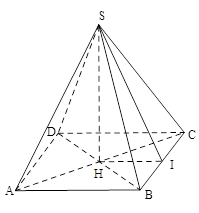
Xét hình chóp tứ giác đều $S.ABCD$ có đường cao
$SH = 35cm$, cạnh $AB = 24cm\,\,$
Gọi $SI$ là đường cao của $\Delta SBC$. Tam giác $SBC$ cân tại $S$ nên $BI = IC$ . Ta có $HI$ là đương trung bình của $\Delta ABC$nên $HI = \dfrac{{AB}}{2} = \dfrac{{24}}{2} = 12\left( {cm} \right)$
Áp dụng định lí Py-ta-go vào tam giác vuông $SHI$ Ta có $S{I^2} = S{H^2} + H{I^2} = {35^2} + {12^2} = 1369 = {37^2}$
Nên $SI = 37\left( {cm} \right)$.
Tính độ dài trung đoạn.

Xét hình chóp tứ giác đều $S.ABCD$ có đường cao
$SH = 35cm$, cạnh $AB = 24cm\,\,$
Gọi $SI$ là đường cao của $\Delta SBC$. Tam giác $SBC$ cân tại $S$ nên $BI = IC$ . Ta có $HI$ là đương trung bình của $\Delta ABC$nên $HI = \dfrac{{AB}}{2} = \dfrac{{24}}{2} = 12\left( {cm} \right)$
Áp dụng định lí Py-ta-go vào tam giác vuông $SHI$ Ta có $S{I^2} = S{H^2} + H{I^2} = {35^2} + {12^2} = 1369 = {37^2}$
Nên $SI = 37\left( {cm} \right)$.
Tính diện tích xung quanh hình chóp.
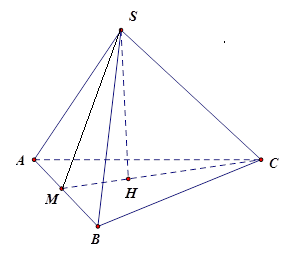
Ta có $SM = CM$ ( đường cao hai tam giác đều và bằng nhau) nên
\(SM = 3\sqrt 3 \) cm
\({S_{xq}} = pd = \dfrac{{6.3}}{2}.3\sqrt 3 = 27\sqrt 3 \) $\left( {c{m^2}} \right)$ .
Tính \(AB\) .
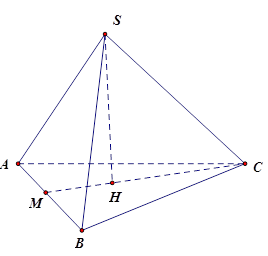
Gọi $M$ là giao điểm của $CH$ và $AB$ ta có \(CM \bot AB\) và $AM = BM$ . Vì \(H\) là trọng tâm \(\Delta ABC\) nên
\(CM = \dfrac{3}{2}CH = \dfrac{3}{2}.2\sqrt 3 = 3\sqrt 3 (cm)\)
Đặt $AB = BC = x$ , ta có \(B{C^2} - M{B^2} = C{M^2}\) (định lý Pytago cho \(\Delta MBC\) ) nên
\({x^2} - {\left( {\dfrac{x}{2}} \right)^2} = {\left( {3\sqrt 3 } \right)^2}hay{\rm{ }}\dfrac{{3{x^2}}}{4} = 27\)
Suy ra $x = 6$ . Vậy $AB = 6cm$ .
Tính \(AB\) .

Gọi $M$ là giao điểm của $CH$ và $AB$ ta có \(CM \bot AB\) và $AM = BM$ . Vì \(H\) là trọng tâm \(\Delta ABC\) nên
\(CM = \dfrac{3}{2}CH = \dfrac{3}{2}.2\sqrt 3 = 3\sqrt 3 (cm)\)
Đặt $AB = BC = x$ , ta có \(B{C^2} - M{B^2} = C{M^2}\) (định lý Pytago cho \(\Delta MBC\) ) nên
\({x^2} - {\left( {\dfrac{x}{2}} \right)^2} = {\left( {3\sqrt 3 } \right)^2}hay{\rm{ }}\dfrac{{3{x^2}}}{4} = 27\)
Suy ra $x = 6$ . Vậy $AB = 6cm$ .
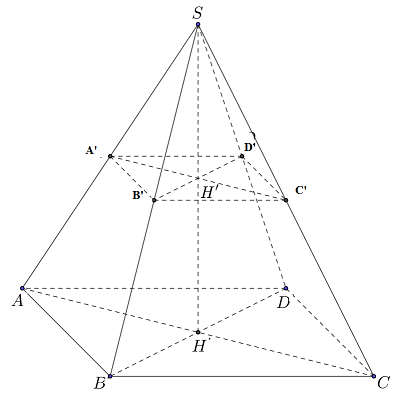
Tính thể tích của hình chóp cụt \(ABCD.A'B'C'D'\) .
Ta có \(SH' = \dfrac{1}{2}SH = \dfrac{1}{2}.6 = 3\,cm\)
Ta có \(SH' = HH'\) nên \(SA' = AA'\) , tương tự \(SB' = BB'\) Suy ra \(A'B' = \dfrac{1}{2}AB = \dfrac{1}{2}.4 = 2\,cm\)
Thể tích hình chóp \(S.A'B'C'D'\) bằng \(\dfrac{1}{3}{.2^2}.3 = 4\,c{m^3}\)
Thể tích hình chóp cụt bằng \(32 - 4 = 28\,c{m^3}\) .
Tính thể tích của hình chóp $S.ABCD$.
Thể tích hình chóp $S.ABCD$ bằng \(\dfrac{1}{3}{.4^2}.6 = 32\,c{m^3}\) .
Tính thể tích của hình chóp $S.ABCD$.

Thể tích hình chóp $S.ABCD$ bằng \(\dfrac{1}{3}{.4^2}.6 = 32\,c{m^3}\) .
Hình chóp tứ giác đều có mặt bên là hình gì?
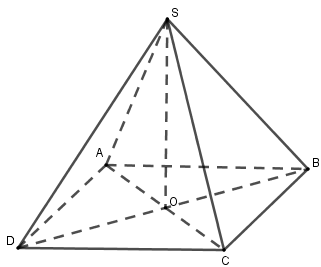
Hình chóp tứ giác đều có các cạnh bên bằng nhau và các cạnh đáy bằng nhau nên mặt bên là những tam giác cân.
Hình chóp lục giác đều có bao nhiêu mặt?

Hình lục giác đều có \(6\) mặt bên và 1 mặt đáy nên có tất cả \(7\) mặt.
Diện tích xung quanh của hình chóp đều bằng
Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy và trung đoạn.
Hình chóp đều có chiều cao \(h\) , diện tích đáy \(S\) . Khi đó, thể tích \(V\) của hình chóp đều bằng
Thể tích của hình chóp đều bằng $\dfrac{1}{3}$ diện tích đáy nhân với chiều cao $V = \dfrac{1}{3}S.h$
( $S$ là diện tích đáy, $h$ là chiều cao).
Một hình chóp tứ giác đều có chiều cao $35\,cm$ , cạnh đáy $24\,cm$ .
Tính độ dài trung đoạn.

Xét hình chóp tứ giác đều $S.ABCD$ có đường cao
$SH = 35cm$, cạnh $AB = 24cm\,\,$
Gọi $SI$ là đường cao của $\Delta SBC$. Tam giác $SBC$ cân tại $S$ nên $BI = IC$ . Ta có $HI$ là đương trung bình của $\Delta ABC$nên $HI = \dfrac{{AB}}{2} = \dfrac{{24}}{2} = 12\left( {cm} \right)$
Áp dụng định lí Py-ta-go vào tam giác vuông $SHI$ Ta có $S{I^2} = S{H^2} + H{I^2} = {35^2} + {12^2} = 1369 = {37^2}$
Nên $SI = 37\left( {cm} \right)$.
Một hình chóp tứ giác đều có chiều cao $35\,cm$ , cạnh đáy $24\,cm$ .
Tính diện tích toàn phần của hình chóp tứ giác đều.
Chu vi đáy bằng $24.4 = 96\left( {cm} \right)$
${S_{xq}} = p.d = \dfrac{{96}}{2}.37 = 1776\left( {c{m^2}} \right)$
Diện tích đáy bằng $24.24 = 576\left( {c{m^2}} \right)$
Diện tích toàn phần $1776 + 576 = 2352\left( {c{m^2}} \right)$
Một hình chóp tứ giác đều có thể tích bằng $200\,c{m^3}$, chiều cao bằng $12\,cm$. Tính độ dài cạnh bên.
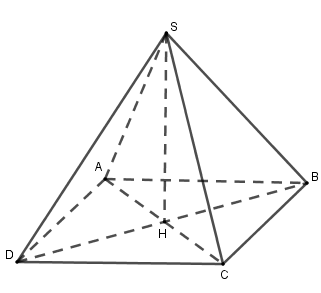
Xét hình chóp tứ giác đều $S.ABCD$ có $V = 200c{m^3}$, đường cao $SH = 12cm$.
Ta có \(V = \dfrac{1}{3}{S_d}.h \) $\Rightarrow {S_d} = \dfrac{{3V}}{{SH}} = \dfrac{{3.200}}{{12}} = 50\left( {c{m^2}} \right)$
Tức là $B{C^2} = 50$
Tam giác $BHC$ vuông cân nên $H{B^2} + H{C^2} = B{C^2}$ hay $2H{C^2} = B{C^2}$ hay $2H{C^2} = 50$.
Suy ra $H{C^2} = 25$.
$S{C^2} = S{H^2} + H{C^2} = {12^2} + 25 = 169 = {13^2}.$ Vậy $SC = 13cm.$
Vậy độ dài cạnh bên là \(13\,cm\) .
Thể tích của hình chóp tứ giác đều có chiều cao $6$ cm, cạnh đáy $4$ cm là
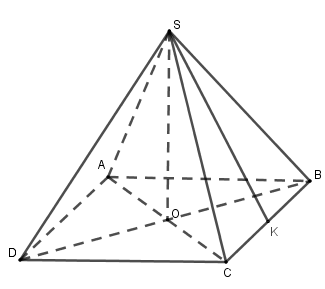
Đáy của chóp tứ giác đều là hình vuông nên diện tích đáy là \(S = {4^2} = 16\,c{m^2}\) .
Thể tích cần tìm là \(V = \dfrac{1}{3}.6.16 = 32\,c{m^3}\) .
Tính diện tích xung quanh của hình chóp cụt tứ giác đều có các cạnh đáy bằng $6cm$ và $8cm$ , chiều cao của mặt bên bằng $5cm$ .
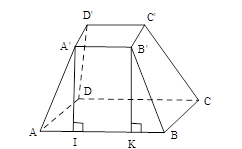
Mặt bên hình chóp cụt tứ giác đều là hình thang cân nên diện tích một mặt bên bằng \(\dfrac{{\left( {6 + 8} \right).5}}{2} = 35\,(c{m^2})\)
Hình chóp cụt tứ giác đều có \(4\) mặt bên bằng nhau nên diện tích xung quanh bằng $35.4 = 140\left( {c{m^2}} \right)$ .
Cho hình chóp tam giác đều $S.ABC$ có các mặt là các tam giác đều. Gọi $SH$ là đường cao của hình chóp, $HC = 2\sqrt 3 cm$.
Tính \(AB\) .

Gọi $M$ là giao điểm của $CH$ và $AB$ ta có \(CM \bot AB\) và $AM = BM$ . Vì \(H\) là trọng tâm \(\Delta ABC\) nên
\(CM = \dfrac{3}{2}CH = \dfrac{3}{2}.2\sqrt 3 = 3\sqrt 3 (cm)\)
Đặt $AB = BC = x$ , ta có \(B{C^2} - M{B^2} = C{M^2}\) (định lý Pytago cho \(\Delta MBC\) ) nên
\({x^2} - {\left( {\dfrac{x}{2}} \right)^2} = {\left( {3\sqrt 3 } \right)^2}hay{\rm{ }}\dfrac{{3{x^2}}}{4} = 27\)
Suy ra $x = 6$ . Vậy $AB = 6cm$ .
Cho hình chóp tam giác đều $S.ABC$ có các mặt là các tam giác đều. Gọi $SH$ là đường cao của hình chóp, $HC = 2\sqrt 3 cm$.
Tính diện tích xung quanh hình chóp.

Ta có $SM = CM$ ( đường cao hai tam giác đều và bằng nhau) nên
\(SM = 3\sqrt 3 \) cm
\({S_{xq}} = pd = \dfrac{{6.3}}{2}.3\sqrt 3 = 27\sqrt 3 \) $\left( {c{m^2}} \right)$ .

