Câu hỏi:
3 năm trước
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng \(6\,cm\). Thể tích hình chóp gần nhất với số nào dưới đây?
Trả lời bởi giáo viên
Đáp án đúng: a
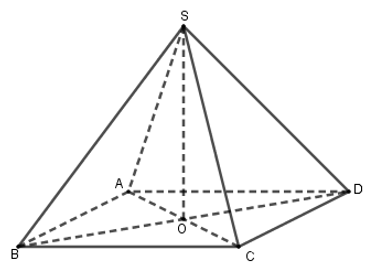
Diện tích đáy: \({S_{ABCD}} = {6^2} = 36\left( {c{m^2}} \right)\).
Xét tam giác \(ABC\) có: \(A{C^2} = A{B^2} + B{C^2} = {6^2} + {6^2} = 72\) \( \Rightarrow AC \approx 8,5\)\( \Rightarrow AO = \dfrac{1}{2}AC = 4,25\)
Tam giác \(SOA\) vuông tại \(O\) có: \(S{A^2} = S{O^2} + O{A^2}\) \( \Leftrightarrow {6^2} = S{O^2} + 4,{25^2}\) \( \Leftrightarrow SO = 4,25\)
Thể tích hình chóp: \(V = \dfrac{1}{3}{S_{ABCD}}.SO = \dfrac{1}{3}.36.4,25 = 51\left( {c{m^3}} \right)\).
Hướng dẫn giải:
Sử dụng công thức tính thể tích chóp tam giác đều \(V = \dfrac{1}{3}Sh\).

