Câu hỏi:
2 năm trước
Một hình chóp tứ giác đều có thể tích bằng \(64\,c{m^3}\), chiều cao bằng \(12\,cm\). Tính độ dài cạnh đáy.
Trả lời bởi giáo viên
Đáp án đúng: c
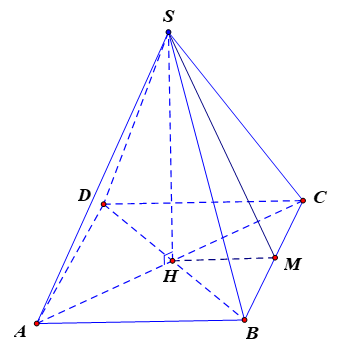
Xét hình chóp tứ giác đều \(S.ABCD\) có: \(V = 64c{m^3}\), chiều cao $h=12cm$.
Ta có: \(V = \dfrac{1}{3}{S_d}.h \Rightarrow \) \({S_d} = \dfrac{{3V}}{{SH}} = \dfrac{{3.64}}{{12}} = 16\left( {c{m^2}} \right)\)
Tức là \(B{C^2} = 16 \Rightarrow BC = 4\)
Vậy độ dài cạnh đáy là \(4\,cm\).
Hướng dẫn giải:
Sử dụng công thức thể tích hình chóp \(V = \dfrac{1}{3}Sh\).

