Trả lời bởi giáo viên
Đáp án đúng: c
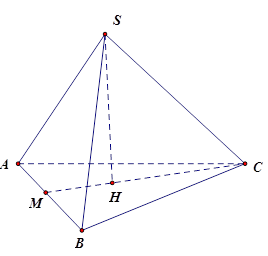
Gọi $M$ là giao điểm của $CH$ và $AB$ ta có \(CM \bot AB\) và $AM = BM$ . Vì \(H\) là trọng tâm \(\Delta ABC\) nên
\(CM = \dfrac{3}{2}CH = \dfrac{3}{2}.2\sqrt 3 = 3\sqrt 3 (cm)\)
Đặt $AB = BC = x$ , ta có \(B{C^2} - M{B^2} = C{M^2}\) (định lý Pytago cho \(\Delta MBC\) ) nên
\({x^2} - {\left( {\dfrac{x}{2}} \right)^2} = {\left( {3\sqrt 3 } \right)^2}hay{\rm{ }}\dfrac{{3{x^2}}}{4} = 27\)
Suy ra $x = 6$ . Vậy $AB = 6cm$ .
Hướng dẫn giải:
Sử dụng tính chất hình chóp đều và định lý Pytago để tính toán

