Cho đa thức \(P\left( x \right) = {x^2} + mx - 9\) (m là tham số). Tìm giá trị của m để \(x = 1\) là một nghiệm của đa thức \(P\left( x \right)\).
Để \(x = 1\) là nghiệm của \(P\left( x \right) = {x^2} + mx - 9\) ta có:
\(\begin{array}{l}P\left( 1 \right) = 1 + m - 9 = 0\\ \Leftrightarrow m - 8 = 0\\ \Leftrightarrow m = 8\end{array}\).
Vậy \(m = 8\) thì \(x = 1\) là một nghiệm của đa thức \(P\left( x \right)\).
Cho các đa thức \(f(x) = - 3{x^2} + {x^4} + 2x + {x^3} - 4\); \(g(x) = {x^3} - 4{x^2} + {x^4} - 4 + 3x\).
Sắp xếp các đa thức \(f\left( x \right),\,{\rm{ }}g\left( x \right)\) theo lũy thừa giảm dần của biến.
Ta có: \(f(x) = - 3{x^2} + {x^4} + 2x + {x^3} - 4\)\( = {x^4} + {x^3} - 3{x^2} + 2x - 4\)
\(g(x) = {x^3} - 4{x^2} + {x^4} - 4 + 3x \)\(= {x^4} + {x^3} - 4{x^2} + 3x - 4\).
Vậy \(f\left( x \right) = {x^4} + {x^3} - 3{x^2} + 2x - 4;\) \(g\left( x \right) = {x^4} + {x^3} - 4{x^2} + 3x - 4.\)
Cho các đa thức \(f(x) = - 3{x^2} + {x^4} + 2x + {x^3} - 4\); \(g(x) = {x^3} - 4{x^2} + {x^4} - 4 + 3x\).
Tìm đa thức h(x) sao cho \(h(x) = f(x) - g(x)\).
\(h(x) = f(x) - g(x) = \)(\({x^4} + {x^3} - 3{x^2} + 2x - 4\))\( - ({x^4} + {x^3} - 4{x^2} + 3x - 4)\)
\( = {x^4} + {x^3} - 3{x^2} + 2x - 4\)\( - {x^4} - {x^3} + 4{x^2} - 2x + 4\)
\( = {x^2} - x\).
Vậy \(h\left( x \right) = {x^2} - x\).
Cho các đa thức \(f(x) = - 3{x^2} + {x^4} + 2x + {x^3} - 4\); \(g(x) = {x^3} - 4{x^2} + {x^4} - 4 + 3x\).
Có bao nhiêu nghiệm của đa thức \(h(x)\) với \(h(x)=f(x)-g(x)\).
Theo câu trước ta có: \(h(x)=f(x)-g(x)= {x^2} - x\)
Ta có: \(h(x) = 0 \Leftrightarrow {x^2} - x = 0\).
\( \Leftrightarrow x(x - 1) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\)
Vậy đa thức h(x) các các nghiệm là: \(x = 0;x = 1.\)
Cho tam giác \(ABC\) vuông tại \(A,\) phân giác \(BD\) ( \(D \in AC\)), từ \(D\) kẻ \(DE \bot BC\,(E \in BC)\).
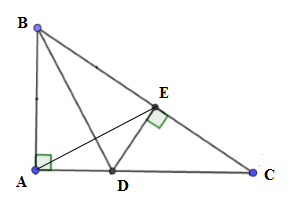
Chọn câu đúng.
Xét hai tam giác vuông ABD và EBD có:
BD chung; \(\widehat {ABD} = \widehat {EBD}\) (gt)
\( \Rightarrow \Delta ABD = \Delta EBD \,(ch - gn)\)
\( \Rightarrow BA = BE;DA = DE\) (hai cạnh tương ứng)
Suy ra: \(\Delta ABE\) cân tại \(B\) và \(\Delta ADE\) cân tại D.
Cho tam giác \(ABC\) vuông tại \(A,\) phân giác \(BD\) ( \(D \in AC\)), từ \(D\) kẻ \(DE \bot BC\,(E \in BC)\).

So sánh độ dài các đoạn thẳng \(AD\) và \(DC\).
Do tam giác \(DEC\) vuông tại \(C\) nên \(DC > DE;\) mà \(DE = AD\) (theo câu trước)
Suy ra \(DC > AD.\)
Cho tam giác \(ABC\) vuông tại \(A,\) phân giác \(BD\) ( \(D \in AC\)), từ \(D\) kẻ \(DE \bot BC\,(E \in BC)\).

Biết \(BE = 12cm;AD = 5cm\). Tính độ dài đoạn thẳng \(BD.\)
Áp dụng định lý Py-ta-go vào tam giác vuông BDE có:
\(B{D^2} = B{E^2} + D{E^2} \Leftrightarrow B{D^2} = BE{}^2 + A{D^2}\) (do \(AD = DE\) (theo câu trước))
\( \Leftrightarrow BD = \sqrt {B{E^2} + A{D^2}} = \sqrt {{{12}^2} + {5^2}} = \sqrt {169} = 13(cm)\).
Cho \(a > 2;b > 2\). Chọn câu đúng.
Do \(a > 2;\,b > 2 \Rightarrow a - 1 > 1 > 0;b - 1 > 1 > 0\)
\( \Rightarrow (a - 1)(b - 1) > 1 \Leftrightarrow ab - a - b + 1 > 1 \Leftrightarrow ab > a + b\).
Cho đa thức \(f\left( x \right)\) thỏa mãn: \(\left( {x - 1} \right).f\left( x \right) = \left( {x + 2} \right)f\left( {x + 3} \right)\) với mọi \(x.\) Tìm 5 nghiệm của đa thức \(f\left( x \right)\).
Ta có: \(f\left( x \right)\) thỏa mãn: \(\left( {x - 1} \right).f\left( x \right) = \left( {x + 2} \right)f\left( {x + 3} \right)\).
Nếu \(f\left( a \right) = 0 \Rightarrow a\) là một nghiệm của \(f\left( x \right)\).
Vì \(\left( {x - 1} \right).f\left( x \right) = \left( {x + 2} \right)f\left( {x + 3} \right)\) đúng với mọi x.
+) Ta thấy \(x = 1\) thì ta có:
\(\left( {1 - 1} \right)f\left( 1 \right) = \left( {1 + 2} \right)f\left( {1 + 3} \right)\)
\(\Rightarrow 0.f\left( 1 \right) = 3.f\left( 4 \right)\)
\(\Rightarrow 0 = 3.f\left( 4 \right)\)
\( \Rightarrow f\left( 4 \right) = 0\)
\(Hay\,\,\,\,x = 4\) là một nghiệm của \(f\left( x \right)\)
+) Với \(x = - 2\) ta được:
\(\left( { - 2 - 1} \right).f\left( { - 2} \right) = \left( { - 2 + 2} \right).f\left( { - 2 + 3} \right)\)
\( \Rightarrow - 3.f\left( { - 2} \right) = 0\)
\( \Rightarrow f\left( { - 2} \right) = 0\)
Hay \( x = - 2\) là một nghiệm của \(f\left( x \right)\)
+) Với \(x = 4\) ta được:
\(\left( {4 - 1} \right).f\left( 4 \right) = \left( {4 + 2} \right).f\left( {4 + 3} \right)\)
\( \Rightarrow 3.f\left( 4 \right)\)\( = \,6.f\left( 7 \right)\)
\( \Rightarrow 0= 6f\left( 7 \right)\)\( \Rightarrow f\left( 7 \right) = 0\)
\(Hay\,\,\,\,x = 7\) là một nghiệm của \(f\left( x \right)\)
+) Với \(x = 7\) ta tìm được \(f\left( {10} \right) = 0\,\,\,\,hay\,\,\,x = 10\) là một nghiệm của \(f\left( x \right)\)
+) Với \(x = 10\) ta tìm được \(f\left( {13} \right) = 0\,\,\,hay\,\,\,\,x = 13\) là một nghiệm của \(f\left( x \right)\)
Vậy 5 nghiệm của \(f\left( x \right)\) là: \(x \in \left\{ {4; - 2;7;10;13} \right\}\).

