Câu hỏi:
3 năm trước
Cho tam giác \(ABC\) vuông tại \(A,\) phân giác \(BD\) ( \(D \in AC\)), từ \(D\) kẻ \(DE \bot BC\,(E \in BC)\).
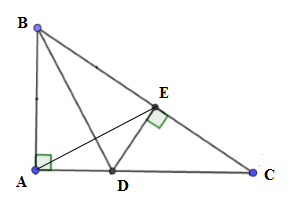
Biết \(BE = 12cm;AD = 5cm\). Tính độ dài đoạn thẳng \(BD.\)
Trả lời bởi giáo viên
Đáp án đúng: b
Áp dụng định lý Py-ta-go vào tam giác vuông BDE có:
\(B{D^2} = B{E^2} + D{E^2} \Leftrightarrow B{D^2} = BE{}^2 + A{D^2}\) (do \(AD = DE\) (theo câu trước))
\( \Leftrightarrow BD = \sqrt {B{E^2} + A{D^2}} = \sqrt {{{12}^2} + {5^2}} = \sqrt {169} = 13(cm)\).
Hướng dẫn giải:
Sử dụng định lý Pytago: “Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông”.

