Câu hỏi:
3 năm trước
Tam giác \(ABC\) vuông tại A, kẻ \(AH \bot BC\) tại H. Biết \(\widehat {ABC} = {65^0}\). Số
đo \(\widehat {HAC}\) là:
Trả lời bởi giáo viên
Đáp án đúng: d
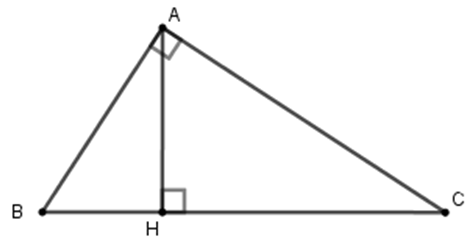
Xét tam giác \(AHB\) vuông tại \(H,\) có \(\widehat {BAH} + \widehat {ABH} = {90^0}\) mà \(\widehat {ABH} = \widehat {ABC} = {65^0}\)
Nên \(\widehat {BAH} = {90^0} - \widehat {ABH} = {90^0} - {65^0}\) \( = {25^0}\)
Lại có \(\widehat {BAH} + \widehat {HAC} = {90^0}\) nên \(\widehat {HAC} = {90^0} - \widehat {BAH} = {90^0} - {25^0}\) \( = {65^0}.\)
Vậy \(\widehat {HAC} = {65^0}.\)
Hướng dẫn giải:
Sử dụng hai góc phụ nhau có số đo bằng \({90^0}.\)
Trong tam giác vuông, hai góc nhọn phụ nhau.

