Trả lời bởi giáo viên
Đáp án đúng: d
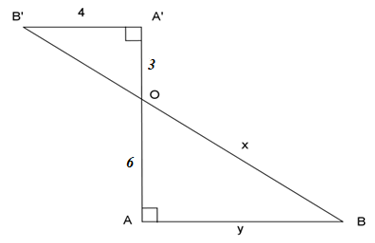
Áp dụng định lý Py-ta-go cho tam giác vuông \(OA'B'\), ta có:
\(\begin{array}{l}OA{'^2} + A'B{'^2} = OB{'^2}\\ \Leftrightarrow {3^2} + {4^2} = OB{'^2}\\ \Leftrightarrow OB{'^2} = 25\\ \Rightarrow OB' = 5\end{array}\)
\(A'B' \bot AA',\;AB \bot AA' \Rightarrow A'B'\parallel AB\) (Theo định lý từ vuông góc đến song song)
Áp dụng định lý Ta-let, ta có:
\(\dfrac{{OA'}}{{OA}} = \dfrac{{OB'}}{{OB}} = \dfrac{{A'B'}}{{AB}}\)
\( \Rightarrow \dfrac{3}{6} = \dfrac{5}{x} = \dfrac{4}{y}\)\( \Rightarrow \left\{ \begin{array}{l}x = \dfrac{{5.6}}{3} = 10\\y = \dfrac{{6.4}}{3} = 8\end{array} \right.\) hay \(x - y = 10 - 8 = 2\).
Hướng dẫn giải:
Bước 1: Tính \(OB'\) dựa vào định lý Pytago từ đó áp dụng định lý talet tìm ra tỉ lệ thức phù hợp.
Bước 2: Biến đổi tỉ lệ thức tìm ra giá trị \(x,y\) và suy ra \(x - y\).
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
