Trả lời bởi giáo viên
Đáp án đúng: b
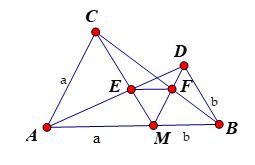
Vì các tam giác \(AMC\) và \(BMD\) đều nên \(\widehat {BMD} = \widehat {MAC} = 60^\circ \Rightarrow MD{\rm{//}}AC\) (vì hai góc ở vị trí đồng vị)
Vì \(MD{\rm{//}}AC\) nên theo hệ quả định lý Talet cho hai tam giác \(DEM\) và \(AEC\) ta có \(\dfrac{{ME}}{{EC}} = \dfrac{{MD}}{{AC}} = \dfrac{b}{a}\)
Suy ra
\(\begin{array}{l}\dfrac{{ME}}{{EC}} = \dfrac{b}{a} \Rightarrow \dfrac{{ME}}{{ME + EC}} = \dfrac{b}{{b + a}}\\ \Rightarrow \dfrac{{ME}}{a} = \dfrac{b}{{b + a}} \Rightarrow ME = \dfrac{{ab}}{{b + a}}\end{array}\)
Tương tự \(MF = \dfrac{{ba}}{{a + b}}\) .
Vậy \(ME = MF = \dfrac{{ab}}{{b + a}}\).
Hướng dẫn giải:
Bước 1: Chứng minh \(MD{\rm{//}}AC\)
Bước 2: Sử dụng định lý Ta-let và tính chất tỉ lệ thức.