Cho hình thang \(ABCD\) \(\left( {AB{\rm{//}}CD} \right)\) có \(BC = 15\,cm,AD = 12\,cm\). Điểm \(E\) thuộc cạnh \(AD\) sao cho \(AE = 4\). Qua \(E\) kẻ đường thẳng song song với \(CD\), cắt \(BC\) ở \(F\). Tính độ dài \(BF\).

Cho hình vẽ, trong đó \(DE{\rm{//}}BC\), \(AE = 12,\,DB = 18,\,AC = 36\). Độ dài \(AB\) bằng:

Chọn câu trả lời đúng:

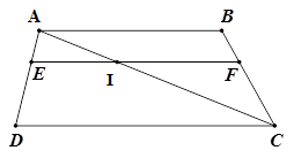
Cho hình thang \(ABCD\) (\(AB{\rm{//}}CD\)), \(O\) là giao điểm của \(AC\) và \(BD\). Xét các khẳng định sau:

(I) \(\dfrac{{OA}}{{OC}} = \dfrac{{AB}}{{CD}}\)                          (II) \(\dfrac{{OB}}{{OC}} = \dfrac{{BC}}{{AD}}\)                        (III) \(OA.OD = OB.OC\)

Số khẳng định đúng trong các khẳng định trên là:

Cho biết \(M\) thuộc đoạn thẳng \(AB\) thỏa mãn \(\dfrac{{AM}}{{MB}} = \dfrac{3}{8}\). Đặt \(\dfrac{{AM}}{{AB}} = k\), số \(k\) thỏa mãn điều kiện nào dưới đây?

Tam giác \(MEF\) là tam giác gì? Chọn đáp án đúng nhất.

Đặt \(MA = a,MB = b\). Tính \(ME,MF\) theo \(a\) và \(b\).

Đặt \(MA = a,MB = b\). Tính \(ME,MF\) theo \(a\) và \(b\).

Cho hình vẽ, trong đó \(AB{\rm{//}}CD\) và \(DE = EC\). Trong các khẳng định sau, có bao nhiêu khẳng định đúng?

(I) \(\dfrac{{AK}}{{EC}} = \dfrac{{KB}}{{DE}}\)      (II) \(\dfrac{{AK}}{{AB}} = \dfrac{{DE}}{{DC}}\)

(III) \(\dfrac{{AO}}{{OC}} = \dfrac{{AB}}{{DC}}\)           (IV) \(\dfrac{{OK}}{{OE}} = \dfrac{{AB}}{{CD}}\)