Câu hỏi:
2 năm trước
Chọn câu trả lời đúng: Cho hình bên, biết \(ED \bot AB,AC \bot AB\), tìm \(x\):
Trả lời bởi giáo viên
Đáp án đúng: a
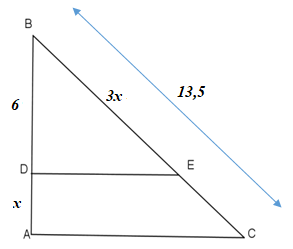
Ta có: \(ED \bot AB,AC \bot AB\)\( \Rightarrow DE{\rm{//}}AC\) (từ vuông góc đến song song), áp dụng định lý Talet, ta có:
\(\dfrac{{BD}}{{DA}} = \dfrac{{BE}}{{EC}}\) \( \Rightarrow \dfrac{6}{x} = \dfrac{{3x}}{{13,5 - 3x}}\) \( \Leftrightarrow 6\left( {13,5 - 3x} \right) = x.3x\) \( \Leftrightarrow 81 - 18x = 3{x^2}\) \( \Leftrightarrow 3{x^2} + 18x - 81 = 0\)
\( \Leftrightarrow {x^2} + 6x - 27 = 0\) \( \Leftrightarrow {x^2} + 9x - 3x - 27 = 0\) \( \Leftrightarrow x\left( {x + 9} \right) - 3\left( {x + 9} \right) = 0\) \( \Leftrightarrow \left( {x + 9} \right)\left( {x - 3} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x + 9 = 0\\x - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 9\left( {loai} \right)\\x = 3\left( {TM} \right)\end{array} \right.\)
Vậy \(x = 3\).
Hướng dẫn giải:
Bước 1: Áp dụng định lý Talet để lập được tỉ lệ thức phù hợp
Bước 2: Biến đổi tỉ lệ thức để tìm ra giá trị \(x\).
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
