Câu hỏi:
3 năm trước
Cho tam giác \(ABC\), điểm \(D\) trên cạnh \(BC\) sao cho \(BD = \dfrac{3}{4}BC\), điểm \(E\) trên đoạn thẳng \(AD\) sao cho \(AE = \dfrac{1}{3}AD\). Gọi \(K\) là giao điểm của \(BE\) với \(AC\). Tỉ số \(\dfrac{{AK}}{{KC}}\) là:
Trả lời bởi giáo viên
Đáp án đúng: c
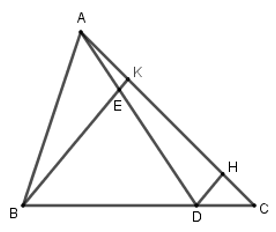
Qua \(D\) kẻ đường thẳng song song với \(BK\) cắt \(AC\) ở \(H\).
Theo định lí Ta-let:
Do \(EK//DH\) nên \(\dfrac{{AK}}{{KH}} = \dfrac{{AE}}{{ED}} = \dfrac{1}{2}\) (1)
Do \(DH//BK\) nên \(\dfrac{{KH}}{{KC}} = \dfrac{{BD}}{{BC}} = \dfrac{3}{4}\) (2)
Từ (1) và (2) suy ra \(\dfrac{{AK}}{{KH}}.\dfrac{{KH}}{{KC}} = \dfrac{1}{2}.\dfrac{3}{4} = \dfrac{3}{8}\).
Vậy \(\dfrac{{AK}}{{KC}} = \dfrac{3}{8}\).
Hướng dẫn giải:
- Qua \(D\) kẻ đường thẳng song song với \(BK\) cắt \(AC\) ở \(H\).
- Sử dụng định lý Ta-let suy ra tỉ số.