Câu hỏi:
2 năm trước
Cho tam giác \(ABC\). Một đường thẳng song song song với \(BC\) cắt các cạnh \(AB\) và \(AC\) theo thứ tự tại \(D\) và \(E\). Qua \(E\) kẻ đường thẳng song song với \(CD\), cắt \(AB\) ở \(F\). Biết \(AB = 16, AF = 9\), độ dài \(AD\) là:
Trả lời bởi giáo viên
Đáp án đúng: c
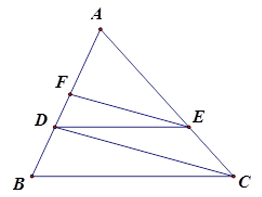
Áp dụng định lí Ta-lét :
Với \({\rm{EF//}}CD\) ta có: \(\dfrac{{AF}}{{AD}} = \dfrac{{AE}}{{AC}}\).
Với \(DE{\rm{//}}BC\) ta có: \(\dfrac{{AE}}{{AC}} = \dfrac{{AD}}{{AB}}\).
Suy ra \(\dfrac{{AF}}{{AD}} = \dfrac{{AD}}{{AB}}\), tức là \(AF.AB = A{D^2}\).
Vậy \(9.16 = A{D^2}\)\( \Leftrightarrow A{D^2} = 144 \Leftrightarrow AD = 12\) (cm).