Cho hai đường tròn \(\left( {O;6\,cm} \right)\) và \(\left( {O';2\,cm} \right)\) cắt nhau tại \(A,B\) sao cho \(OA\) là tiếp tuyến của \(\left( {O'} \right)\). Độ dài dây \(AB\) là
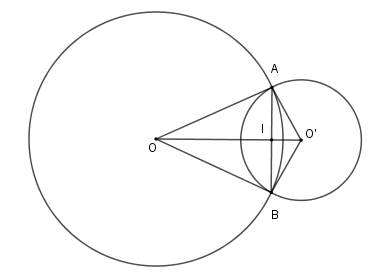
Vì \(OA\) là tiếp tuyến của \(\left( {O'} \right)\) nên \(\Delta OAO'\) vuông tại \(A\).
Vì \(\left( O \right)\) và \(\left( {O'} \right)\) cắt nhau tại \(A,B\) nên đường nối tâm \(OO'\) là trung trực của đoạn \(AB\).
Gọi giao điểm của \(AB\) và \(OO'\) là \(I\) thì \(AB \bot OO'\) tại \(I\) là trung điểm của \(AB\)
Áp dụng hệ thức lượng trong tam giác vuông \(OAO'\) ta có
\(\dfrac{1}{{A{I^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O'{A^2}}} = \dfrac{1}{{{6^2}}} + \dfrac{1}{{{2^2}}} \Rightarrow AI = \dfrac{{3\sqrt {10} }}{5}\,cm \Rightarrow AB = \dfrac{{6\sqrt {10} }}{5}\,cm\)
Cho hai đường tròn \(\left( {O;10cm} \right)\) và \(\left( {O';5cm} \right)\) cắt nhau tại \(A\) và \(B\) . Tính đoạn nối tâm \(OO'\), biết rằng \(AB = 8\,cm\) và \(O\) và \(O'\) nằm cùng phía đối với \(AB\) . (làm tròn đến chữ số thập phân thứ nhất)
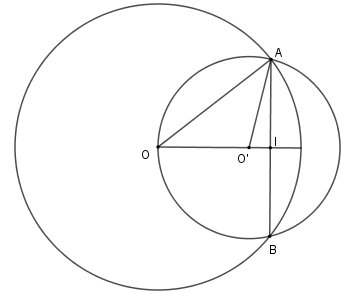
Ta có: \(AI = \dfrac{1}{2}AB = 4\,cm\)
Theo định lý Pytago ta có
\(O{I^2} = O{A^2}-A{I^2} = {10^2} - {4^2} = 84\) \( \Rightarrow \) \(OI = 2\sqrt {21} \) và \(O'I = \sqrt {O'{A^2} - I{A^2}} = \sqrt {{5^2} - {4^2}} = 3\)
Do đó: \(OO' = OI-O'I = 2\sqrt {21} -3 \approx 6,2\left( {cm} \right)\) .
Chọn câu đúng.
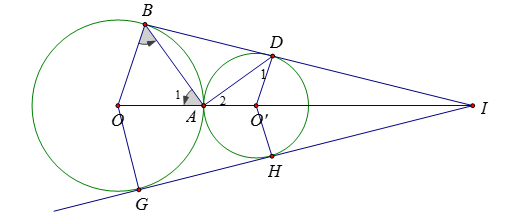
Gọi giao điểm của \(OO'\) và \(GH\) là \(I'\)
Ta có \(OG{\rm{ }}//{\rm{ }}O'H\) ( do cùng vuông góc\(GH\) )
Theo định lí Ta let trong tam giác \(OGI'\) ta có \(\dfrac{{I'O}}{{I'O'}} = \dfrac{{OG}}{{O'H}} = \dfrac{R}{{R'}}\) hay \(\dfrac{{I'O}}{{I'O'}} = \dfrac{{OI}}{{O'I}} = \dfrac{R}{{R'}}\)
\(\; \Rightarrow I'\) trùng với \(I\)
Vậy \(BD,{\rm{ }}OO'\) và \(GH\) đồng quy.
Tính \(OI\) theo \(R\) và \(R'\)
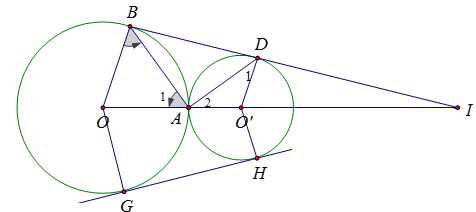
Xét tam giác \(IOB\) có \(OB//O'D\left( {gt} \right)\)
Áp dụng định lí Ta-let ta có \(\dfrac{{OI}}{{O'I}} = \dfrac{{OB}}{{O'D}} \Leftrightarrow \dfrac{{OI}}{{O'I}} = \dfrac{R}{{R'}}\) mà \(O'I = OI - OO' = OI - \left( {OA + AO'} \right) = OI - \left( {R + R'} \right)\)
Nên \(\dfrac{{OI}}{{OI - \left( {R + R'} \right)}} = \dfrac{R}{{R'}}\) \( \Rightarrow OI.R' = R\left[ {OI - \left( {R + R'} \right)} \right]\) \( \Leftrightarrow OI.R - OI.R' = R\left( {R + R'} \right)\)
\( \Leftrightarrow OI\left( {R - R'} \right) = R\left( {R + R'} \right)\) \( \Leftrightarrow OI = \dfrac{{R\left( {R + R'} \right)}}{{R - R'}}\)
Tính \(OI\) theo \(R\) và \(R'\)

Xét tam giác \(IOB\) có \(OB//O'D\left( {gt} \right)\)
Áp dụng định lí Ta-let ta có \(\dfrac{{OI}}{{O'I}} = \dfrac{{OB}}{{O'D}} \Leftrightarrow \dfrac{{OI}}{{O'I}} = \dfrac{R}{{R'}}\) mà \(O'I = OI - OO' = OI - \left( {OA + AO'} \right) = OI - \left( {R + R'} \right)\)
Nên \(\dfrac{{OI}}{{OI - \left( {R + R'} \right)}} = \dfrac{R}{{R'}}\) \( \Rightarrow OI.R' = R\left[ {OI - \left( {R + R'} \right)} \right]\) \( \Leftrightarrow OI.R - OI.R' = R\left( {R + R'} \right)\)
\( \Leftrightarrow OI\left( {R - R'} \right) = R\left( {R + R'} \right)\) \( \Leftrightarrow OI = \dfrac{{R\left( {R + R'} \right)}}{{R - R'}}\)
Tính diện tích tam giác \(A'B'C'.\)
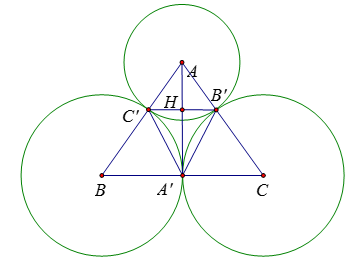
Ta có: \(\dfrac{{AC'}}{{AB}} = \dfrac{{AB'}}{{AC}} = \dfrac{{10}}{{25}} = \dfrac{2}{5}\)
\( \Rightarrow B'C'{\rm{ }}//{\rm{ }}BC\) do đó \(B'C' \bot AA'\)
Lại có: \(\dfrac{{B'C'}}{{BC}} = \dfrac{{AC'}}{{AB}} \Rightarrow \dfrac{{B'C'}}{{30}} = \dfrac{2}{5} \Leftrightarrow B'C' = 12\,cm\)
Xét \(\Delta ABA'\) có \(B'C'{\rm{ }}//{\rm{ }}BC\) nên theo định lý Ta-let ta có \(\dfrac{{AH}}{{A'A}} = \dfrac{{BC'}}{{BA}} \Rightarrow \dfrac{{AH}}{{20}} = \dfrac{{15}}{{25}} \Rightarrow AH = 12\,cm\) (do theo câu trước thì \(AA' = 20\,cm\) )
Diện tích tam giác \(A'B'C'\) là: \(S = \dfrac{1}{2}B'C'.AH = \dfrac{1}{2}.12.12 = 72\,\left( {c{m^2}} \right)\)
Chọn câu đúng nhất.
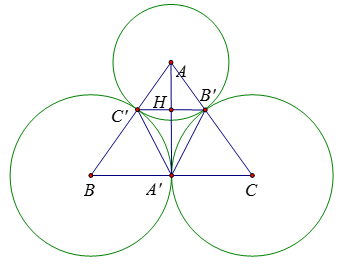
+) Theo tính chất đoạn nối tâm của hai đường tròn tiếp xúc ngoài ta có:
\(AB = BC' + C'A = 25\,cm;{\rm{ }}AC = AB' + B'C = 25\,cm;\) \({\rm{ }}BC = BA' + A'C = 30cm\) và \(A'\) là trung điểm của \(BC\) (vì \(A'B = A'C = 15cm\))
\(\Delta ABC\) cân tại \(A\) có \(AA'\) là đường trung tuyến nên cũng là đường cao
\( \Rightarrow AA' \bot BC\)
\( \Rightarrow AA'\) là tiếp tuyến chung của hai đường tròn (B) và (C)
Xét tam giác \(AA'C\) vuông tại \(A'\) có:
\(\;A'{A^2}\; = {\rm{ }}A{C^2}\; - {\rm{ }}A'{C^2}\; = {\rm{ }}{25^2} - {\rm{ }}{15^2}\; = 400\)\( \Rightarrow A'A{\rm{ }} = {\rm{ }}20\,cm\)
Chọn câu đúng nhất.

+) Theo tính chất đoạn nối tâm của hai đường tròn tiếp xúc ngoài ta có:
\(AB = BC' + C'A = 25\,cm;{\rm{ }}AC = AB' + B'C = 25\,cm;\) \({\rm{ }}BC = BA' + A'C = 30cm\) và \(A'\) là trung điểm của \(BC\) (vì \(A'B = A'C = 15cm\))
\(\Delta ABC\) cân tại \(A\) có \(AA'\) là đường trung tuyến nên cũng là đường cao
\( \Rightarrow AA' \bot BC\)
\( \Rightarrow AA'\) là tiếp tuyến chung của hai đường tròn (B) và (C)
Xét tam giác \(AA'C\) vuông tại \(A'\) có:
\(\;A'{A^2}\; = {\rm{ }}A{C^2}\; - {\rm{ }}A'{C^2}\; = {\rm{ }}{25^2} - {\rm{ }}{15^2}\; = 400\)\( \Rightarrow A'A{\rm{ }} = {\rm{ }}20\,cm\)
Hai đường tròn \(\left( {O;5} \right)\) và \(\left( {O';8} \right)\) có vị trí tương đối với nhau như thế nào biết \(OO' = 12\)
Ta có: \(\left| {{R_1} - {R_2}} \right| = 8 - 5 = 3;\;\;{R_1} + {R_2} = 8 + 5 = 13.\)
\( \Rightarrow \left| {{R_1} - {R_2}} \right| < OO' < {R_1} + {R_2} \Rightarrow \) hai đường tròn cắt nhau.
Cho hai đường tròn \(\left( {O;4cm} \right)\)và \(\left( {I;6cm} \right)\). Biết \(OI = 2cm\). Tìm vị trí tương đối của hai đường tròn.
Ta có: \({R_1} = 6cm;\,\,\,{R_2} = 4cm;\,\,d = 2cm\)\( \Rightarrow {R_1} - {R_2} = d = 2cm.\)
\( \Rightarrow \) hai đường tròn tiếp xúc trong.
Nếu hai đường tròn tiếp xúc với nhau thì số điểm chung của hai đường tròn là
Hai đường tròn tiếp xúc với nhau thì có một điểm chung duy nhất
Dây $AD$ của đường tròn lớn cắt đường tròn nhỏ tại $C$. Khi đó
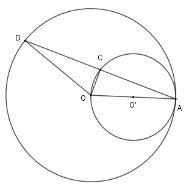
Xét đường tròn $\left( {O'} \right)$ có $OA$ là đường kính và $C \in \left( {O'} \right)$ nên $\Delta ACO$ vuông tại $C$ hay $OC \bot AD$
Xét đường tròn $\left( O \right)$có $OA = OD \Rightarrow \Delta OAD$ cân tại $O$ có $OC$ là đường cao cũng là đường trung tuyến nên $CD = CA$
Vị trí tương đối của hai đường tròn là
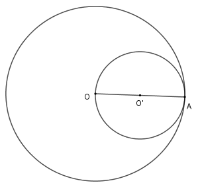
Vì hai đường tròn có một điểm chung là $A$ và $OO' = OA - \dfrac{{OA}}{2} = R - r$ nên hai đường tròn tiếp xúc trong.
Vị trí tương đối của hai đường tròn là

Vì hai đường tròn có một điểm chung là $A$ và $OO' = OA - \dfrac{{OA}}{2} = R - r$ nên hai đường tròn tiếp xúc trong.
Lấy $M$ là trung điểm của $BC$. Chọn khẳng định sai?
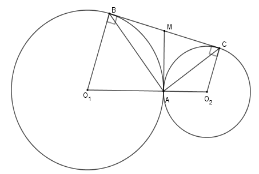
Vì $\Delta ABC$ vuông tại $A$ có $AM$ là trung tuyến nên $AM = BM = DM = \dfrac{{BC}}{2}$
Xét tam giác $BMA$ cân tại $M$ $ \Rightarrow \widehat {MBA} = \widehat {MAB}$, mà $\widehat {{O_1}BA} = \widehat {{O_1}AB}$ (cmt) nên $\widehat {{O_1}BA} + \widehat {MBA} = \widehat {{O_1}AB} + \widehat {MAB} \Rightarrow \widehat {{O_1}AM} = \widehat {{O_1}BM} = 90^\circ $$ \Rightarrow MA \bot A{O_1}$ tại $A$ nên $AM$ là tiếp tuyến của $\left( {{O_1}} \right)$
Tương tự ta cũng có $ \Rightarrow MA \bot A{O_2}$ tại $A$ nên $AM$ là tiếp tuyến của $\left( {{O_2}} \right)$
Hay $AM$ là tiếp tuyến chung của hai đường tròn
Vậy phương án A, C, D đúng. B sai.
Tam giác $ABC$ là
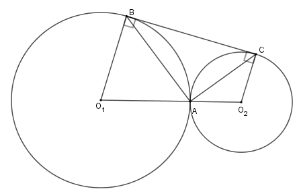
Xét $\left( {{O_1}} \right)$ có ${O_1}B = {O_1}A$
$\Rightarrow \Delta {O_1}AB$ cân tại ${O_1}$
$\Rightarrow \widehat {{O_1}BA} = \widehat {{O_1}AB}$
Xét $\left( {{O_2}} \right)$ có ${O_2}C = {O_2}A $
$\Rightarrow \Delta {O_2}CA$ cân tại ${O_2}$
$\Rightarrow \widehat {{O_2}CA} = \widehat {{O_2}AC}$
Mà $\widehat {{O_1}} + \widehat {{O_2}} = 360^\circ - \widehat C - \widehat B = 180^\circ $
$ \Leftrightarrow 180^\circ - \widehat {{O_1}BA} - \widehat {{O_1}AB} + 180^\circ - \widehat {{O_2}CA} - \widehat {{O_2}AC} = 180^\circ $
$\Leftrightarrow 2\left( {\widehat {{O_1}AB} + \widehat {{O_2}AC}} \right) = 180^\circ $
$ \Rightarrow \widehat {{O_1}AB} + \widehat {{O_2}AC} = 90^\circ $
$ \Rightarrow \widehat {BAC} = 90^\circ $
$\Rightarrow \Delta ABC$ vuông tại $A$.
Tam giác $ABC$ là

Xét $\left( {{O_1}} \right)$ có ${O_1}B = {O_1}A$
$\Rightarrow \Delta {O_1}AB$ cân tại ${O_1}$
$\Rightarrow \widehat {{O_1}BA} = \widehat {{O_1}AB}$
Xét $\left( {{O_2}} \right)$ có ${O_2}C = {O_2}A $
$\Rightarrow \Delta {O_2}CA$ cân tại ${O_2}$
$\Rightarrow \widehat {{O_2}CA} = \widehat {{O_2}AC}$
Mà $\widehat {{O_1}} + \widehat {{O_2}} = 360^\circ - \widehat C - \widehat B = 180^\circ $
$ \Leftrightarrow 180^\circ - \widehat {{O_1}BA} - \widehat {{O_1}AB} + 180^\circ - \widehat {{O_2}CA} - \widehat {{O_2}AC} = 180^\circ $
$\Leftrightarrow 2\left( {\widehat {{O_1}AB} + \widehat {{O_2}AC}} \right) = 180^\circ $
$ \Rightarrow \widehat {{O_1}AB} + \widehat {{O_2}AC} = 90^\circ $
$ \Rightarrow \widehat {BAC} = 90^\circ $
$\Rightarrow \Delta ABC$ vuông tại $A$.
Nếu $BC$ là tiếp tuyến của nửa đường tròn $\left( {O'} \right)$ thì tính $BC$ theo $R$ (với $OA = R$)
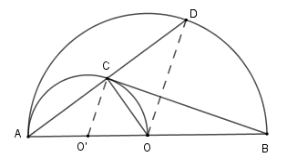
Ta có $OB = R;OO' = \dfrac{R}{2} \Rightarrow O'B = \dfrac{{3R}}{2}$;$O'C = \dfrac{R}{2}$
Theo định lý Pytago ta có $BC = \sqrt {O'{B^2} - O'{C^2}} = \sqrt {\dfrac{{9{R^2}}}{4} - \dfrac{{{R^2}}}{4}} = \sqrt 2 R$
Cho hai đường tròn $\left( {O;R} \right)$ và $\left( {O';r} \right)$ với $R > r$ cắt nhau tại hai điểm phân biệt và $OO' = d$. Chọn khẳng định đúng?
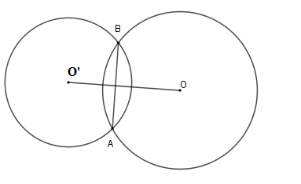
Hai đường tròn $\left( {O;R} \right)$ và $\left( {O';r} \right)$$\left( {R > r} \right)$cắt nhau.
Khi đó $\left( O \right)$ và $\left( {O'} \right)$ có hai điểm chung và đường nối tâm là đường trung trực của đoạn $AB$.
Hệ thức liên hệ $R - r < OO' < R + r$
Cho hai đường tròn $\left( {O;8\,cm} \right)$ và $\left( {O';6cm} \right)$ cắt nhau tại $A,B$ sao cho $OA$ là tiếp tuyến của $\left( {O'} \right)$. Độ dài dây $AB$ là
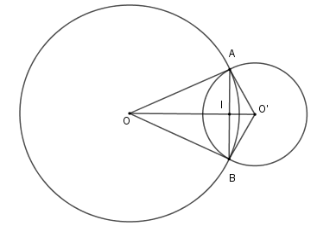
Vì $OA$ là tiếp tuyến của $\left( {O'} \right)$ nên $\Delta OAO'$ vuông tại $A$.
Vì $\left( O \right)$ và $\left( {O'} \right)$ cắt nhau tại $A,B$ nên đường nối tâm $OO'$ là trung trực của đoạn $AB$.
Gọi giao điểm của $AB$ và $OO'$ là $I$ thì $AB \bot OO'$ tại $I$ là trung điểm của $AB$
Áp dụng hệ thức lượng trong tam giác vuông $OAO'$ ta có
$\dfrac{1}{{A{I^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O'{A^2}}} = \dfrac{1}{{{8^2}}} + \dfrac{1}{{{6^2}}} \Rightarrow AI = 4,8\,cm \Rightarrow AB = 9,6\,cm$

