Lấy $M$ là trung điểm của $BC$. Chọn khẳng định sai?

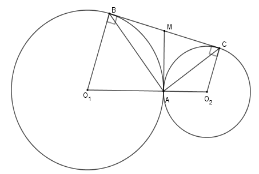
Vì $\Delta ABC$ vuông tại $A$ có $AM$ là trung tuyến nên $AM = BM = DM = \dfrac{{BC}}{2}$

Xét tam giác $BMA$ cân tại $M$ $ \Rightarrow \widehat {MBA} = \widehat {MAB}$, mà $\widehat {{O_1}BA} = \widehat {{O_1}AB}$ (cmt) nên $\widehat {{O_1}BA} + \widehat {MBA} = \widehat {{O_1}AB} + \widehat {MAB} \Rightarrow \widehat {{O_1}AM} = \widehat {{O_1}BM} = 90^\circ $$ \Rightarrow MA \bot A{O_1}$ tại $A$ nên $AM$ là tiếp tuyến của $\left( {{O_1}} \right)$

Tương tự ta cũng có $ \Rightarrow MA \bot A{O_2}$ tại $A$ nên $AM$ là tiếp tuyến của $\left( {{O_2}} \right)$

Hay $AM$ là tiếp tuyến chung của hai đường tròn

Vậy phương án A, C, D đúng. B sai.