Trả lời bởi giáo viên
Đáp án đúng: a
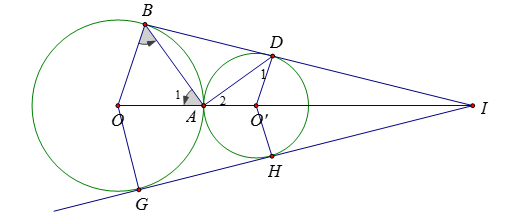
Gọi giao điểm của \(OO'\) và \(GH\) là \(I'\)
Ta có \(OG{\rm{ }}//{\rm{ }}O'H\) ( do cùng vuông góc\(GH\) )
Theo định lí Ta let trong tam giác \(OGI'\) ta có \(\dfrac{{I'O}}{{I'O'}} = \dfrac{{OG}}{{O'H}} = \dfrac{R}{{R'}}\) hay \(\dfrac{{I'O}}{{I'O'}} = \dfrac{{OI}}{{O'I}} = \dfrac{R}{{R'}}\)
\(\; \Rightarrow I'\) trùng với \(I\)
Vậy \(BD,{\rm{ }}OO'\) và \(GH\) đồng quy.
Hướng dẫn giải:
Gọi giao điểm của \(OO'\) và \(GH\) là \(I'\), ta đi chứng minh \(I \equiv I'\)
Sử dụng định lý Ta-lét
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
