Trả lời bởi giáo viên
Đáp án đúng: d
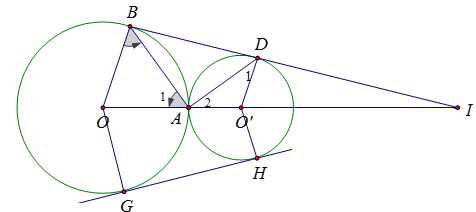
Xét tam giác \(IOB\) có \(OB//O'D\left( {gt} \right)\)
Áp dụng định lí Ta-let ta có \(\dfrac{{OI}}{{O'I}} = \dfrac{{OB}}{{O'D}} \Leftrightarrow \dfrac{{OI}}{{O'I}} = \dfrac{R}{{R'}}\) mà \(O'I = OI - OO' = OI - \left( {OA + AO'} \right) = OI - \left( {R + R'} \right)\)
Nên \(\dfrac{{OI}}{{OI - \left( {R + R'} \right)}} = \dfrac{R}{{R'}}\) \( \Rightarrow OI.R' = R\left[ {OI - \left( {R + R'} \right)} \right]\) \( \Leftrightarrow OI.R - OI.R' = R\left( {R + R'} \right)\)
\( \Leftrightarrow OI\left( {R - R'} \right) = R\left( {R + R'} \right)\) \( \Leftrightarrow OI = \dfrac{{R\left( {R + R'} \right)}}{{R - R'}}\)
Hướng dẫn giải:
Sử dụng định lý Ta-lét và đẳng thức \(\dfrac{a}{b} = \dfrac{c}{d} \Leftrightarrow ad = bc\)
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
